PROPULSION PHOTONIQUE ET REMONTEE DU PERIGEE

PROPULSION PHOTONIQUE, EFFET SUR LA MONTEE DU PERIGEE

CAS : POUSSEE INERTIELLE CONSTANTE

Nous envisageons l'étude du taux de remontée du périgée de l'orbite d'un satellite soumis à l'action de la poussée photonique.

Au départ, on ne se préoccupe pas de la manière dont est générée cette force, ni comment la voile est pilotée pour profiter au mieux de ce type de propulsion.

I NOTATIONS:

Nous traitons LE PROBLEME PLAN avec le soleil constamment dans le plan orbital. Nous nous limitons donc au cas d'une orbite dans l'écliptique ou bien au cas particulier du soleil dans le plan orbital

P : premier axe du repère périfocal, direction du périgée

Q : deuxième axe du repère périfocal PQW

s : angle de la direction des rayons solaires avec P

a : angle d'orientation de la normale n à la voile, avec P

p₀ = 9 10-6 Pa : pression photonique

S surface utile éclairée de la voile

F₀ norme de la force photonique maximale en réflexion spéculaire parfaite

r rendement dans le cas d'une réflexion réelle non totalement spéculaire

F= r F₀ = r p₀ S cos²y force photonique réelle compte tenu du rendement et de l'orientation de la voile

M masse du voilier

II CALCUL DU TAUX INSTANTANE DE MONTEE DU PERIGEE:

La force photonique est réputée très faible et le traitement de son effet propulsif relève des équations de Gauss.

1°) EQUATIONS DE GAUSS POUR a ET e :

Nous rappelons la configuration des axes, les notations et les deux équations indispensables au cas qui nous intéresse.

Les axes locaux à la position courante S sont le radial R, l'orthoradial T dans le plan de l'orbite osculatrice et N normal à ce plan de même sens que le moment cinétique.

Rp, Tp, Np désignent les composantes de l'accélération perturbatrice sur ces axes locaux.

A chaque instant l'orbite osculatrice est caractérisée par ses paramètres orbitaux instantanés notamment a(t) et e(t), permet de calculer l'altitude sol du périgée de cette orbite r_p = a ( 1 - e ).

L'optimisation consiste tout simplement à rendre maximal le taux de croissance de l'altitude du périgée à chaque instant. Pour ce faire nous partons des équations de Gauss:

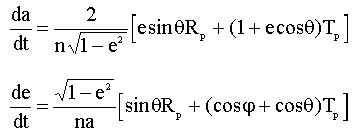
où j est l'anomalie excentrique, n le moyen mouvement, et q l'anomalie vraie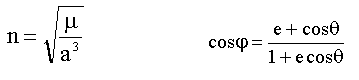

2°) EQUATION SPECIALE DE GAUSS POUR LE PERIGEE :

Nous pouvons écrire:

et en déduire sans difficulté, partant de dr_p=(1-e)da-ade

3°) CALCULS DU TAUX INSTANTANE DE MONTEE DU PERIGEE :

On transforme les équations de Gauss. Rappelons que Rp, Tp, Np sont les composantes de l'accélération perturbatrice, r le rendement, a l'angle avec P d'orientation de la normale à la voile.

On rappelle :

Condition nécessaire d'éclairement de la bonne face

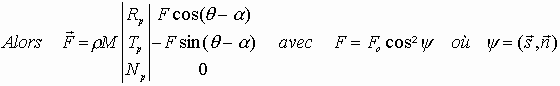
donc

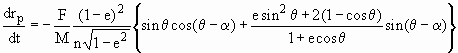
Intéressons nous à l'évolution suivant l'angle polaire q (anomalie vraie)

On rappelle:

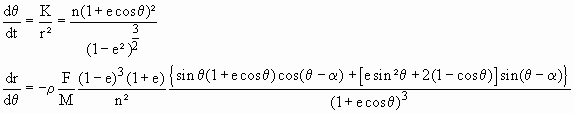
Ce taux est représenté ci-dessous, pour un rendement de 0.8 et a=2.2 rd, en fonction de q.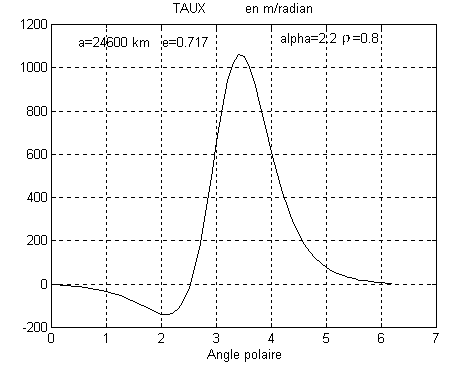

On constate u ne zone où ce taux est <0, ce qui nous amènera à une optimisation plus précise du vol.

III CAS UNE FORCE PHOTONIQUE INERTIELLEMENT CONSTANTE:

On suppose donc un pilotage qui maintient une orientation galiléenne fixe de la voile sur une période du mouvement. L'angle a est constant ainsi que la force F.

Le lecteur réalisera les calculs et simplifications intermédiaires pour aboutir après une intégration sur une période orbitale, au résultat suivant :

Sur une période orbitale, la variation d'altitude du périgée est :

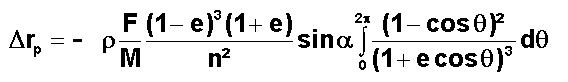
1°) TAUX ALGEBRIQUE DE MONTEE DU PERIGEE PAR TOUR :

Un calcul de l'intégrale est possible par la méthode des résidus en opérant le changement de variable classique z=exp(iq) et en achevant par une intégration sur le cercle unité.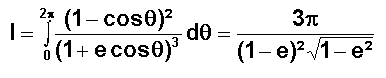

NB : Validité vérifiée par un calcul numérique sous logiciel MATLAB, voir note 1.

On obtient ainsi un résultat analytique du taux de remontée du périgée :

NB: Formule très générale dans le système solaire en adaptant po qui dépend notamment de la distance au soleil

Nous reconnaissons le rendement r, les caractéristiques orbitales avec n et e, une caractéristique essentielle de la voile son rapport S/M , le pilotage avec la position soleil donnée par s , son efficacité avec po et l'orientation de la voile par a.

2°) EXEMPLE 1:

Pour une orbite GTO ( a=24582 km, e=0.71524, n=1.638110-⁴ rd/s ), de périgée 622 km ( tir Ariane 5 ), un rendement photonique 80%, soleil transverse à droite vu de la trajectoire ascendante (a = 270° ), une voile de 100 m² pour une masse de 100 kg, le taux de remontée maximum ( pleine lumière arrière s = a =60° ) est de

1767 m/tour donc sur 38536 s de la période, soit 1.7 km/tour

3962 m/jour, soit dirons nous 3.96 km/jour

Sur la période favorable de 1 mois, avec un rendement photonique de 80%, on peut espérer une remontée du périgée de 100 km environ.

Voir note 2

3°) TAUX ALGEBRIQUE DE MONTEE DU PERIGEE PAR JOUR :

Plus satisfaisant est le taux journalier, dans la mesure où le soleil est très lentement mobile par rapport à la Terre ( environ 1°/jour)

On trouve alors compte tenu de T=2p/n et J=86400 s ( jour solaire moyen )

ATTENTION : Formule valable pour une propulsion photonique circumterrestre.

Nous reconnaissons le rendement r, les caractéristiques orbitales avec n et e, la caractéristique essentielle de la voile son rapport S/M , le pilotage avec la position soleil donnée par s , son efficacité avec po et l'orientation de la voile par a.

Valeur confirmée par le graphe plus loin qui donne le taux de montée optimal dans un pilotage "lumière arrière" sur la portion utile de la trajectoire.

MONTEE AMELIOREE SUR UNE LONGUE PERIODE

L'étude du taux de montée du périgée en fonction de la position q sur l'orbite montre à l'évidence qu'on peut améliorer la montée du périgée en ne gardant que les portions de trajectoire où le taux est positif.

On se mettra donc en drapeau là où le taux local de montée du périgée est<0.

NB 1 : sous matlab on peut rechercher l'unique zéro de la fonction ( il semble qu'il n'y en ait qu'un) par z = zero('f2',pi);

NB 2: M Chiavassa a étudié de manière très fine la fonction implicite qui définit le zéro q0(a) ( unicité à confirmer) de

NOTES POUR LES UTILISATEURS DE MATLAB:

NOTE 1 : On intègre entre 0 et 2p la fonction f3(x) définie par le fichier texte f3.m

function y=f3(x); e=0.71524;y=(1-cos(x)).^2./(1+e.*cos(x)).^3;0;end.

CALCUL : I=quad8('f2',0,2*pi); REPONSE ===> I=166.307

NOTE 2 : On intègre entre 0 et 2p la fonction f2(x) définie par le fichier texte f2.m

function y=f2(x);

% Cette fonction donne en fonction de l'angle polaire x=teta le taux instantané de montée

% du périgée en m/rd, pour les conditions particulières ci-dessous

F0=9e-6;S=100;M=100;a=24582;e=0.71524;r=0.8;n=(39.86e4/a^3)^0.5;alpha=3*pi/2;

y=-sin(x).*cos(x-alpha)-(e.*sin(x).*sin(x)+2*(1-cos(x))).*sin(x-alpha)./(1+e.*cos(x));

y=-r*F0*S/M*(1-e)^3*(1+e)/n^2*y./((1+e.*cos(x)).*(1+e.*cos(x)));

end

CALCUL : I=quad8('f3',0,2*pi); REPONSE ===> I=1762.9

Guiziou Robert janvier 2003