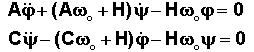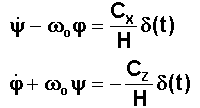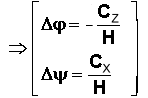|
STABILISATION PAR MOMENT CINETIQUE EMBARQUE |
|
|
CONTENU : Mis à jour novembre 2001, revu sept 2011 |
|
|
|
|
|
|
|
|
NB
: Le lecteur se reportera au cours sur le mouvement de Poinsot, pour revoir les définitions et conventions d'écriture utilisées dans
cette page.
Dans
tout ce qui suit, nous traitons le cas d'un satellite supposé corps solide;
possédant un moment cinétique embarqué.
On
dira qu'un satellite possède un moment cinétique embarqué lorsqu'il est équipé
d'ACTIONNEURS 1 AXE appelés ROUES DE REACTIONS, sous forme de 1 à 3 rotors,
tournant chacun autour d'un axe dont les paliers sont fixes par rapport à la
structure du satellite.
Un moteur prenant appui sur le
satellite agit, sur commande de détecteurs, pour faire varier la vitesse angulaire
du rotor. Comme le processus ne génère que des efforts internes, le moment
cinétique total Satellite + roues reste constant. Le PRINCIPE DU CONTRÔLE est
donc celui d'un ECHANGE DE MOMENT CINETIQUE
entre les roues et le satellite.
Le
vecteur rotation est ainsi modifié et l'attitude aussi.
On
distingue 2 équipements différents fonctionnant sur le même principe.
Les ROUES DE REACTIONS, "travaillant" autour du
zéro.
Les VOLANTS D'INERTIE fonctionnant autour d'une vitesse
non nulle.
La
vitesse de rotation est mesurée par comptage des impulsions en provenance des
enroulements.
3°) CMG (
Control Moment Gyro ):
Ces
actionneurs utilisent aussi une roue, dont la vitesse reste constante. Par
contre l'axe de la rotation peut varier sous commande, faisant ainsi varier le
moment cinétique satellite par échange de moment cinétique. Voir
cours et problème sur ce site.
4°)
EFFET DE REACTION:
Sur
le plan mécanique, dans tous les cas l'échange de moment cinétique à bilan nul,
s'opère par REACTION. Le moteur qui commande
l'actionneur s'appuie sur le satellite et crée sur ce dernier un couple qui a
pour effet de modifier le mouvement de rotation du satellite .
5°)
DOMAINE D'APPLICATION :
La
technique du moment cinétique embarqué grâce à la raideur gyroscopique, est
utilisée pour les géostationnaires et les orbites basses. La raideur
gyroscopique limite les conséquences de pannes.
Cependant
ce SCAO n'est pas applicable ou du moins coûte cher, pour des satellites présentant
de moments d'inertie élevés( gros satellites ou satellites très dissymétriques
avec une grande inertie transverse.
De
nombreuses applications pratiques utilisent un satellite asservi au repère
orbital local, en particulier les satellites d'imagerie spatiale.
1°) REPERE ORBITAL LOCAL :
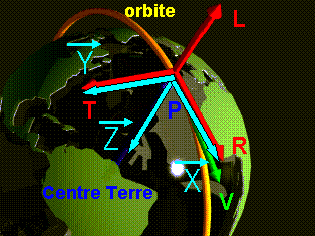
A
gauche une excellente visualisation, provenant du site SPOT4, a été utilisée et
adaptée pour définir le repère orbital local.
Entièrement
défini par la position P et le vecteur vitesse V.
a)
Roulis-Lacet-Tangage:
La
géocentrique Terre-satellite est la direction L de lacet.
L'axe
T de tangage est l'unitaire du produit vectoriel de V et L
L'axe
R, dit de roulis, dans le sens de la vitesse( sur orbite quasi circulaire)
complète la base L T R.
b)
Repère local :
Par
habitude le repère orbital local a pour axes X =
R, Z = -L et Y=T complétant la base directe XYZ. La pulsation orbitale vaut
alors -wo sur Y.
4°)
EXEMPLES :
Rien
ne vaut le cas réel. Vous pouvez aller consulter l'excellent site de SPOT4 et en particulier le contrôle d'attitude à
l'adresse :
http://spot4.cnes.fr/spot4_fr/attitude.htm
NOTE ( Citation à partir d'un document publié) : Le système d'imagerie de la
famille SPOT nécessite un pointage terre à 0°.15. Le satellite doit garder une
de ses faces invariablement pointée vers la terre. Pour ce faire il est en
rotation à la pulsation orbitale wO autour
de l'axe Y de tangage.
La
principale contrainte pour la qualité géométrique des images est de maintenir
toute autre vitesse résiduelle en dessous de 0.001 °/s
Le
contrôle d'attitude de SPOT comprend des roues à réaction, des bobines
magnétiques ( magnétocoupleurs ), des senseurs solaires et
terrestre, des gyromètres et des propulseurs à hydrazine.
2°) REPERAGE ROULIS-LACET EN
CONTROLE LONG TERME:
Pour
les angles ( voir cas des petits angles ), plaçons nous dans le cas du mouvement
libre. La raideur gyroscopique et l'évolution très lente du moment cinétique,
font que ce vecteur paraît inertiellement fixe.
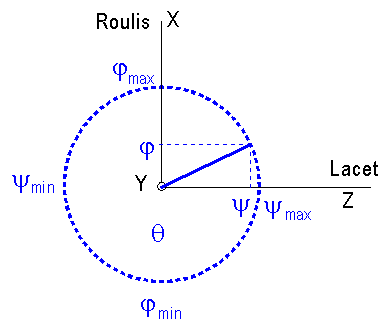
Le
satellite est considéré comme un moment cinétique pur, et le tangage q autour de Y est supposé parfaitement maîtrisé. Lors
de son déplacement long terme, sur son orbite circulaire, à la pulsation wo, le moment cinétique, vu du
satellite, en axes satellite, décrit un cône d'axe Y. L'extrémité de H décrit
dans un plan parallèle au plan (Z, X ) un cercle, dessiné ci-dessous.
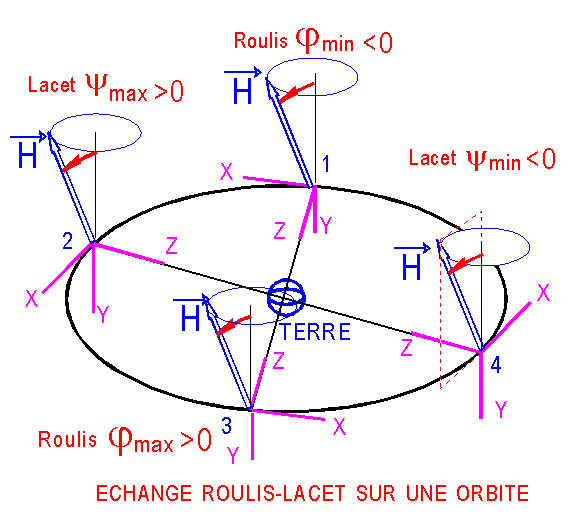
Le
demi-angle d'ouverture du cône, suivant la position sur l'orbite, apparaît soit
:
-
comme un dépointage de roulis autour de l'axe X en position1( roulis j <0, minimum ), en position3( roulis j >0, maximum )
-
comme un dépointage de lacet autour de l'axe Z en position2( lacet y >0, maximum ), en position4( lacet y >0, minimum ).
C'est
cette propriété qu'on nomme ECHANGE ROULIS LACET sur le long terme. Une
conséquence favorable et intéressante est qu'en contrôlant l'un des deux
angles, on contrôle automatiquement l'autre, ce qui réduit le nombre de
capteurs et d'actuateurs.
Le
théorème du moment cinétique donne :
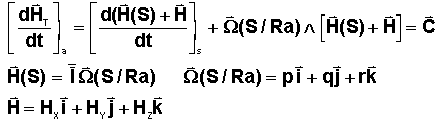
Tous
calculs effectués en axes satellite il vient :
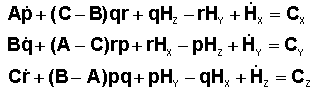
L'étude
se limite à celle du pointage terre.
1°) DEFINITION SCAO N DOF (N = 1,
2, 3 ) :
"DOF"
= Degrees Of Free = Degrés De Liberté. Expliquons sa signification à partir du
moment cinétique qui possède 3 composantes . Dans le cas du pointage Terre le
vecteur H doit rester constamment normal au plan orbital. On impose donc Hx =
Hy = 0 et Hz = H. Ainsi aucun degré de liberté n'est accordé à aucune
composante, puisque toutes sont fixées. Il y a 0 DOF.
On
peut ainsi libérer 1 2 ou 3 composantes.
2°) EQUATIONS DU CONTRÔLE 0 DOF:
Les
hypothèses : pointage
terre( HX = HZ = 0, HY = - H ) et
petits angles de roulis-lacet-tangage( mode courant de stabilisation )
permettent de simplifier le vecteur rotation et les équations:
ATTENTION :
le signe de la rotation orbitale peut changer suivant la direction de Y normal
au plan orbital.
Avec
nos conventions : j roulis /X, y
lacet /Z et q tangage /Y
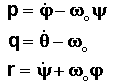
On
notera qu'en court terme on pourra négliger les termes contenant wo.
Avec
les simplifications résultant des hypothèses les équations deviennent :
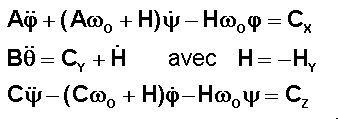
a)
CONTRÔLE TANGAGE ET SATURATION:
L'équation
de tangage en q montre clairement, d'une part un
découplage d'avec les autres angles et aussi l'action directe par effet de
réaction de la dérivée de H ou de - Hy, effet qui apparaît comme un couple de
réaction ( c'est le but recherché ).
Tous
les types de commande sont alors possibles les plus courants et classiques
étant :
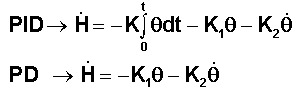
Par
exemple pour un contrôle PD et un couple perturbateur de la forme Cy = G + Cpy coswot, avec
une composante constante G en axes satellites, il vient :
La
solution du système fait apparaître un biais résiduel sur q, qui reporté sur le moment cinétique montre une
croissance en module du moment cinétique, c'est le PHENOMENE
DE SATURATION :
b)
MOUVEMENT LIBRE LACET-ROULIS :
Les
équations du système libre sont découplées vérifient le système :
|
I |
|
Pour
calculer les 2 fréquences propres de ce système manifestement stable et
conservatif, nous formons l'équation aux pulsations propres w, le calcul classique donne :
Il
ne faut pas chercher loin pour découvrir que les 2 pulsations propres du
mouvement sont :
La
pulsation w1 très lente est associée au
mouvement long terme( grande période ) alors que w2 beaucoup plus rapide décrira le mouvement court terme(courte période ).
Comme
la solution générale du mouvement libre est une combinaison des 2 mouvements
propres sinusoïdaux, on peut tracer l'allure de la courbe décrite par
l'extrémité du moment cinétique et qui représente l'évolution du couple
lacet-roulis avec échange de valeurs tout au long de l'orbite.
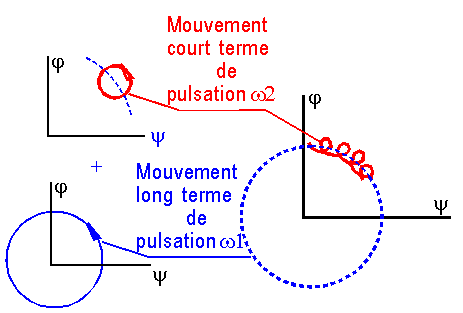
c)
MOUVEMENT REEL LACET-ROULIS :
Les
dessins plus bas montrent mieux qu'une longue explication le rôle des divers
moments cinétiques.
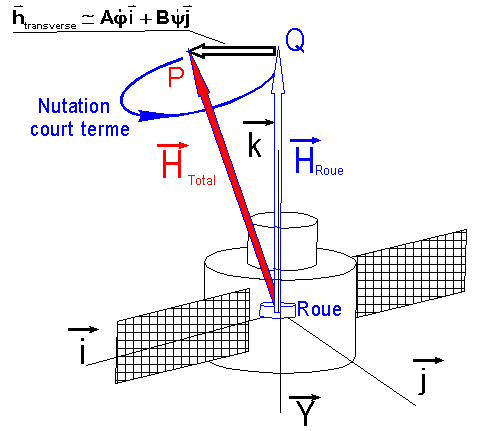
Le
vecteur htransverse( en noir ) est le moment cinétique perturbateur.
P est l'extrémité du moment cinétique total et Q celui du moment cinétique
roue.
Sous
l'effet de perturbations possédant une composante constante en axes satellites,
l'allure du mouvement général en lacet-roulis ressemble à celle du dessin
ci-dessous.
En
pointillé est figuré la trajectoire, long terme, moyenne, du moment cinétique
total HT( en rouge ), d'extrémité P, ce mouvement est très lent.
Sur le
dessin de droite est matérialisé le mouvement de Q, extrémité du moment
cinétique de la roue, mouvement de nutation à pulsation w2.
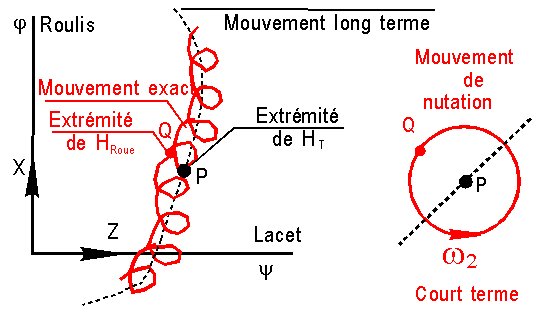
Le
mouvement réel est la composée des 2 mouvements, la trajectoire est décrite en
rouge
On
peut donc en déduire que le lacet et le roulis divergent lentement et
nécessitent un contrôle.
1°)
EQUATIONS DU CONTRÔLE LONG TERME :
Le
MOUVEMENT LONG TERME EST CELUI DU MOMENT CINETIQUE
TOTAL HT. En effet le couple des perturbations externes est
évidemment petit et la vitesse de l'extrémité de HT est très faible.
Le
contrôle long terme est celui qui s'opère à la pulsation w1 de grande période ( de l'ordre de 2
heures ). Les vitesses sont petites et les accélérations encore plus petites et
négligeables . Donc le système décrivant ce mouvement s'écrit simplement :
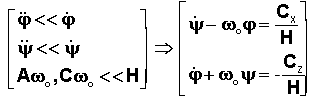
On
retrouve tout naturellement la pulsation propre w1 égale wo.
2°)
EFFETS DES COUPLES PERTURBATEURS :
Il
n'est pas question de faire le bilan de toutes les perturbations, la plupart
ayant déjà été décrites sur ce site.
Cependant,
elles peuvent se classer en 2 catégories, celles qui comportent un couple
constant en axes satellites et celles qui comportent un couple constant en axes
inertiels.
a)
Cas d'un couple constant en axes satellites :
Rappelons
les équations les plus générales et supposons CX, CZ
constants, par exemple <0.
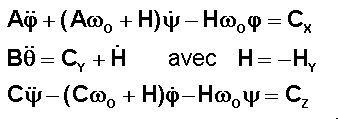
Le
système différentiel présente une solution particulière constante, et
une solution générale combinaison des 2 oscillations propres( une lente et une
rapide).
L'effet
du couple constant se traduit donc par un décalage du centre du mouvement j-y long terme.
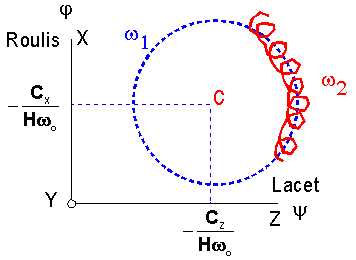
a) Cas d'un couple inertiel
constant :
Pour
simplifier ne gardons qu'un couple inertiel constant G dans le plan orbital supposé fixe. Alors, au cours
du temps ce couple voit ses composantes en axes satellites varier
sinusoïdalement à la pulsation orbitale wo.
Comme
le second membre du système général oscille à une fréquence égale à une
fréquence propre, les mathématiques nous apprennent qu'il y a résonance, se
traduisant pour j et y, par une solution particulière de la forme
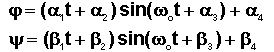
Ce
qui se traduit, sur le mouvement j & y par une trajectoire divergente en forme de spirale d'Archimède.
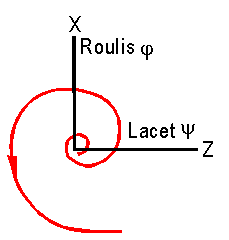
Naturellement,
la réalité met en œuvre des couples de toute nature et la trajectoire tient
donc des 2 types, comme indiqué par un croquis en IV 2°).
3°)
UN EXEMPLE DE CONTRÔLE :
CONTRAINTE
A RESPECTER EN CONTINU :
Conserver
le moment cinétique total, le moment cinétique roue et l'axe Y, colinéaires. Ou
encore p = q = r = 0 quel que soit t et xyz confondus avec XYZ.
LES
MOYENS :
a)
Détection sur un seuil roulis maximum, par exemple, et déclenchement de
la séquence de contrôle
b)
Déplacement de HT , sur contrôle long terme, jusqu'à l'amener
dans la position désirée.
Une
conséquence immédiate est que le moment cinétique H de la roue s'écarte de HT
et donc s'amorce une précession d'angle important.
c)
Réduction à zéro de la nutation, sur contrôle court terme, tout en
conservant HT en place.
4°)
REALISATION DU CONTRÔLE ACTIF :
Comme
roulis et lacet s'échangent sur le mouvement lent, la détection s'opère par
exemple sur le roulis au franchissement d'un seuil de vitesse angulaire.
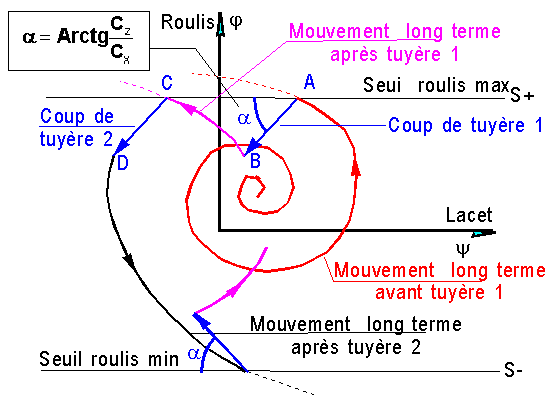
Un "coup de tuyère impulsionnel
d' angle de biaisage a " est alors délivré ramenant
le point ( j, y ) dans une zone acceptable.
|
Angle de biaisage a |
|
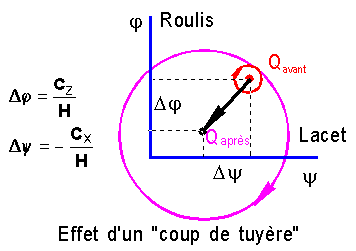
CALCULS :
Supposons
une détection j>0,
y>0. Une action
tuyère est exercée durant un temps dt
de l'ordre de 50 à 100 ms, avec des couples CX et CZ , en
axes satellites, vérifiant un biais a.
Seules les dérivées sont prises en compte dans une processus impulsionnel,
analogue à une percussion.
|
|
|
A RETENIR
: L'effet d'un coup de tuyère est de déplacer l'extrémité Q du moment cinétique
total et d'augmenter le rayon de la nutation du moment cinétique H de la roue autour
de HT.
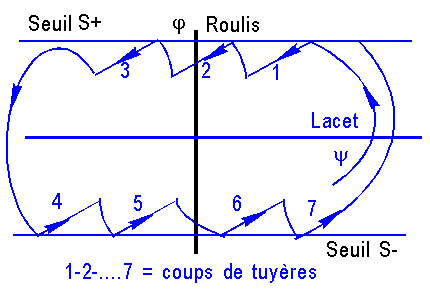
Une
étude poussée montrerait qu'un bon choix du biais, et du seuil, conduit à un
cycle limite, comme suggéré ci-dessous.
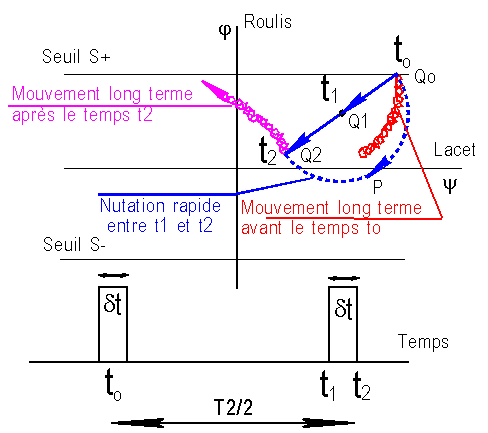
ADAPTATION DU CONTRÔLE LONG TERME POUR ANNULER LA NUTATION :
Nous
avons signalé qu'en déplaçant le moment cinétique total, on créait
automatiquement une nutation plus importante, avec une période déjà rencontrée,
qu'on a appelléeT2, associée à la pulsation court terme w2.
La
"ruse" du contrôle de la nutation, consiste à délivrer le coup de
tuyère en 2 temps de durée dt/2, espacés
de T2/2, grâce à 2 "tops" facilement programmables. Ainsi,
comme le montre la figure ci-dessous, le moment cinétique HT(extrémité
Q )total et celui H(extrémité P ) de la roue se retrouvent en coïncidence( aux
erreurs de fonctionnement près), ce qui supprime la nutation.
5°)
LIMITES DE LA METHODE :
Le
contrôle en quasi continu, demande un nombre très élevé d'activations de
tuyères, avec un risque très pénalisant de panne en "tuyère ouverte".
La
précision atteinte par la détection sur seuils n'est pas excellente, de plus
les erreurs d'alignement soit de la roue soit des senseurs, se répercutent
naturellement sur l'attitude.
Guiziou Robert août 2000, revu
novembre 2001, sept 2011