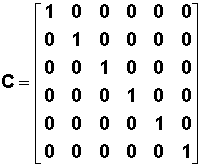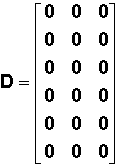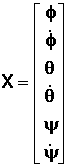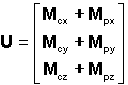|
CONTROLE D'ATTITUDE PAR MAGNETOCOUPLEURS |
|
CONTENU : Mis à jour 8 février 1999, revu avril 2012, juin 2014 Notations et conventions | Calcul
du couple créé | Equations du SCAO | Mise
sous forme canonique | Matrice de gain |Exemple
de spécifications | |
|
|
Voir
les pages consacrées à une application à un nanosatellite |
|
Ce
chapitre est consacré au contrôle actif de l'attitude d'un satellite par magnétocoupleurs.
Nous nous plaçons dans la configuration d'une stabilisation trois axes d'un
satellite, sur orbite circulaire, par rapport au repère orbital. Les écarts
angulaires sont donc supposés petits.
IDEE DIRECTRICE : Réaliser un contrôle de l'attitude
satellite par des couples internes, sans dépense d'énergie stockée et sans
consommation d'ergols.
On
utilise des bobines alimentées par des courants adéquats ( seuls les panneaux
solaires interviennent et l'alimentation est durable, grâce aux batteries ).
La
création de couples nécessitent un champ magnétique externe, or il est présent
certes faible, sous la forme du champ magnétique terrestre. On se limitera donc
à des couples petits, dans le cadre de petits dépointages angulaires
Le
candidat idéal est le MAGNETOCOUPLEUR.
REMARQUES :
Les
magnétocoupleurs peuvent aussi être utilisés, pour de très petits satellites, à
réduire les vitesses angulaires consécutives au lancement. Deux techniques
peuvent être utilisées :
1
– Contrôle par la dérivée du champ magnétique, appelée loi en Bpoint Voir
Brevet de M Damilano Voir
une application à un nanosatellite
2
– Contrôle par une régulation dite
Boussole de’ M Philippe Laurens Voir Brevet de
M Laurens Voir
une application à un nanosatellite
3
– Les magnétocoupleurs peuvent aussi être associés à une roue de réaction Voir
un exemple théorique
1°) Notations et conventions :
a)
Données :
On
appelle ou on rappelle:
o
IR,
IT,IL les inerties en roulis, tangage et lacet.
o
F, q,
y les angles de roulis,
tangage et lacet supposés petits dans le contrôle d'attitude.
o
wo la pulsation orbitale constante
pour une orbite circulaire de rayon r.
Le
repère orbital, dans le cas d'une orbite
circulaire est X, Y, Z avec X unitaire de la vitesse, Z unitaire de la
verticale locale, Y complète le repère
On
notera le vecteur champ magnétique terrestre ( vecteur B ) par ses composantes
dans le repère orbital local XYZ, donc en fonction de la position
courante du satellite, au rayon vecteur r et au temps t, ce calcul peut être
soit analytique avec un modèle embarqué. Les composantes peuvent aussi être
restituées par une mesure du champ à l'aide de magnétomètres. Dans tous les cas
on a:
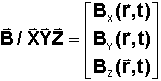
L'électronique
de bord et les capteurs utilisés doivent élaborer un MOMENT MAGNETIQUE
GLOBAL M en utilisant des moments magnétiques par axes, grâce à des bobines
commandées par des courants bien calculés.
b)
Réflexion
sur l'efficacité magnétique
Comme
le couple de commande Mc est un produit vectoriel, son module est maximum quand
les 2 vecteurs M et B sont orthogonaux. Ne pouvant pas changer B, il faut donc
construire M normal à B, puisque la partie de ce moment magnétique colinéaire à
B est inefficace. On utilise pour ce faire un vecteur annexe m pour l'instant non précisé, mais qui va devenir en fait la
commande. Cette optimisation du moment magnétique permet d’économiser de l’énergie.
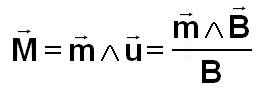

Si
on détaille le couple actif mécanique on observe que le vecteur m pourrait apparaître comme une commande amplifiée par
le module du champ magnétique B, par contre le second terme est moins
prévisible et demande une étude plus poussée

Sur
cette idée ( mais d'autres auraient pu être choisies ), un pseudo moment
magnétique ( au sens mécanique de couple ) de commande est élaboré par le
calculateur, par exemple en loi proportionnelle dérivée:
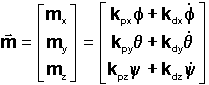
On
note alors que les angles de dépointage sont traités sur les axes respectifs F sur x, q sur y et j sur z, par des commandes
proportionnelles dérivées classiquement amplifiées
D'autres
commandes peuvent naturellement être imaginées.
EXEMPLE
: sur une orbite circulaire proche d'une orbite polaire, on peut dire que le
champ magnétique est dans le plan orbital. Ainsi si on choisi de ne traiter que
le tangage et le lacet, en oubliant le roulis, le terme ![]() disparaît quasiment, supprimant des termes éventuels de couplage
déstabilisants.
disparaît quasiment, supprimant des termes éventuels de couplage
déstabilisants.
2°) Couple dû aux
magnétocoupleurs :
Le
satellite est équipé de magnétomètres( liés au satellite), mesurant in situ les
composantes en axes satellite du champ magnétique terrestre. Des
capteurs de positions angulaires ( senseurs ) et des gyromètres de mesure
de vitesses angulaires associés à une électronique de bord, permettent
d'élaborer les fonctions mx my mz, puis Mx My Mz, et donc les courants à
injecter dans trois bobines suivant les 3 axes pour obtenir le moment
magnétique de commande M.
Le
moment général M du dipôle équivalent s'écrit
sous forme vectorielle :
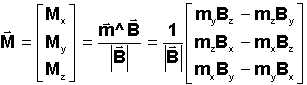
Le
vecteur champ magnétique terrestre calculé dans la base satellite en fonction
des paramètres angulaires et des composantes de B dans le repère orbital, est
dans le cas des petits angles de dépointage :
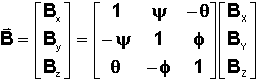
donnant
le couple de commande ci-dessous, obtenu en explicitant le double produit vectoriel:

ce
couple de contrôle agissant sur le satellite est donné par ses composantes dans
les axes satellites. En dernier ressort c'est m( mx my mz ) qui apparaît comme
la commande.
Le
moment total des perturbations extérieures autres que gravitationnelles est :
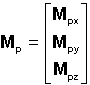
On
consultera, pour évaluer les couples perturbateurs, les ouvrages spécialisés ou
le cours fourni sur ce site.
On
s'intéressera tout particulièrement aux couples d'origine aérodynamiques et on
s'apercevra probablement du rôle important joué par la position du centre de
poussée par rapport au centre de masse.
Les
équations de comportement se présentent sous la forme générale ci-dessous:

où
les quantités du second membre se calculent comme indiqué plus haut.
- Indice c pour commande
- Indice p pour perturbations ( gravitationnelles
non comprises puisqu'elles sont utilisées par le gradient de gravité déjà
inclus dans le premier membre )
Si
par exemple le vecteur d'état du système est noté X,
la perturbation ou la commande(au second membre) est le vecteur d'entrée U =Up
+ Uc, Y le vecteur de sortie,
on a alors par exemple la REPRESENTATION D'ETAT :

Si
en sortie Y=X alors les matrices A, B, C, D s'expriment respectivement ainsi :
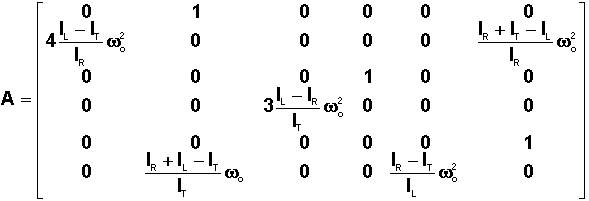
|
|
|
|
Les vecteurs d'état et de commande
sont :
|
|
|
Remarque capitale sur
le rôle des magnétocoupleurs et leur inconvénient:
Les calculs mathématiques ont masqué le rôle important du champ
magnétique terrestre B et sa contribution comme amortisseur des oscillations
des angles de roulis lacet et tangage.
Le lecteur vérifiera lui même que l'expression de Mcx est la
suivante :
![]()
On constate que le premier terme négatif introduit dans
l'équation de roulis en F un rappel élastique et un amortissement. Ces effets sont
favorables à la stabilisation du roulis.
Malheureusement les autres termes de couplage avec le lacet et le
tangage dans l'équation de roulis apparaissent comme perturbateurs et parfois
déstabilisants. C'est donc un inconvénient non négligeable, qui conduit en
pratique à une compensation par roue de réaction, dont le rôle pourrait se
limiter à compenser ces termes parasites.
Naturellement le raisonnement est le même sur les autres axes.
On
parle en général d'une MATRICE DE GAIN notée K dans la boucle de retour d'état.
![]()
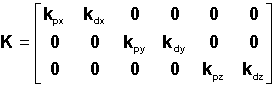
Les
coefficients kpx, ........kdz dans les études réelles, sont à déterminer et
naturellement à optimiser en tenant compte de leur réalité physique et tout en
cherchant à minimiser la consommation en puissance.
4°) Exemple de spécifications
imposées à une mission d'imagerie :
Généralement
l'héliosynchronisme est imposé par une mission d'observation de la Terre
La
technologie des caméras impose donc des spécifications précises en ce qui
concerne:
- La précision de pointage
- Les vitesses angulaires
maximum admissibles pour une prise de vue correcte.
- Caractéristiques techniques du
système de prise de vues:
Z
: Altitude sol de la prise de vue
a : Angle d'ouverture de prise de vue
n
x n : Ensemble de n2 pixels de la matrice carrée CCD
t : temps de prise de vue
k:
0 < k <1 décalage maximum toléré en fraction de pixels de l'image en
début et fin de prise de vue.
d
: Résolution au sol pour 1 pixel
Vous
pourriez montrer par un calcul que les tolérances en vitesses angulaires de
roulis et tangage sont les mêmes et donnent les spécifications suivantes:
![]()
![]()
Pour le lacet par une étude plus
particulière vous établirez
![]()
pour une résolution sol par pixel
![]()
II CHAMP MAGNETIQUE TERRESTRE :
Le
champ magnétique terrestre apparaît comme résultant d'un dipôle
magnétique faisant un angle de 11° avec l'axe de rotation de la Terre
et légèrement décentré. Le pôle sud du dipôle est dans l'hémisphère nord à 78°6
de latitude et 289°55 de longitude ouest, de plus ce dipôle dérive de 0.014°/an
vers l'est et sa force augmente de 0.05% par an. C'est dire la complexité de sa
représentation.
Deux
modèles sont connus:
- IAGA
pour International Association of Geomagnetism and Aeronomy
- IGRF pour International
Geomagnetic Reference Field qui propose un développement
du potentiel magnétique donnant accès au champ magnétique terrestre sous
la forme suivante:
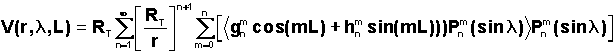
Avec
les notations :
- r rayon vecteur
- L longitude du satellite
- désigne la latitude.
- RT = 6378,135 km: rayon
terrestre équatorial
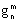 ,
, 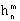 des coefficients connus
fonctions lentement variables de l'année donnés, listés et fournis en
tableaux, dans les ouvrages spécialisés
des coefficients connus
fonctions lentement variables de l'année donnés, listés et fournis en
tableaux, dans les ouvrages spécialisés  sont les fonctions de Legendre
normalisées.
sont les fonctions de Legendre
normalisées.
Pour
une première étude de stabilisation par magnétocoupleurs et une bonne
compréhension du phénomène, nous nous contenterons d'un modèle simple en ne
gardant que les premiers termes du développement soit:
![]()
Nous
obtenons donc les composantes du champ magnétique par
![]()
Br
est la composante radiale
BN la composante tangente au méridien
vers le nord local
BL
la composante vers l'est
Le
calcul donne:

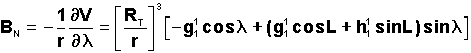
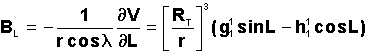
2°) Modèle simplifié du champ
magnétique terrestre :
Nous
commencerons par un modèle encore plus simple sans que cela altère les résultats
généraux de l'étude de contrôle d'attitude.
Hypothèses :
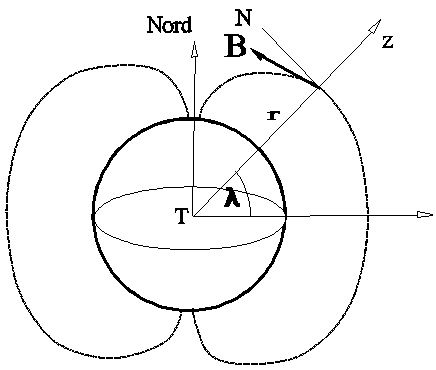
On
assimile le champ magnétique terrestre à celui d'un dipôle magnétique placé
suivant l'axe Nord-Sud de la Terre et présentant ainsi une symétrie de
révolution autour de l'axe de rotation de la Terre.
|
Nous
savons que |
|

où
mo = 4 p 10-7
et K= 6.413 1021
A-m2
N
est la direction locale du Nord (pour nous magnétique et géographique à la fois
avec la simplification adoptée).
Exemple de calcul des composantes de B dans le repère orbital local pour
une orbite héliosynchrone:
Hypothèses:
L'orbite
est supposée circulaire de type héliosynchrone ou du moins d'inclinaison
i>90°.
Le
temps de référence t = 0 est pris à l'un des passages du satellite au noeud N
ascendant (passage de l'hémisphère sud à l'hémisphère nord)
On
appelle j l'angle polaire du satellite compté
à partir du nœud ascendant positivement autour de l'axe de tangage (axe également
porteur du moment cinétique du satellite).
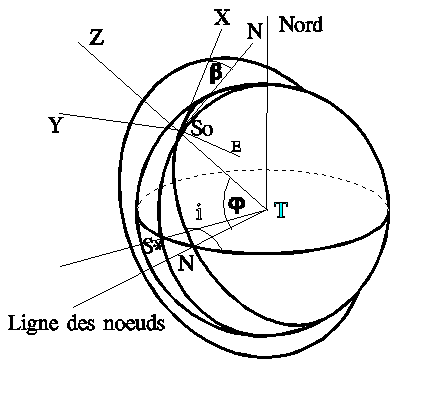
On
appellera b l'angle entre la vitesse (ou
l'axe de roulis X) et la direction N du nord local, est mesuré
positivement autour de la géocentrique Z (Sur la figure trace montante b<0 et i>90°).
![]()
Remarque:
La
simple observation du dessin montre que pour une telle orbite, lorsque la trace
est montante (latitude croissante) -90°< b
<0 et pour une trace descendante (latitude décroissante) -180° < b <-90°.
Calcul
des composantes de B sur X, Y, Z repère local.
On
rappelle les relations de trigonométrie sphérique suivantes :
![]()
De
plus le lecteur se convaincra que le plan E, N est le plan horizontal (E est la
direction de locale de l'est). Il fera attention à l'angle b compté algébriquement dans les calculs de
projection.
La
projection donne alors :
![]()
d'où
les composantes du champ B magnétique en axes du repère orbital local X, Y, Z.
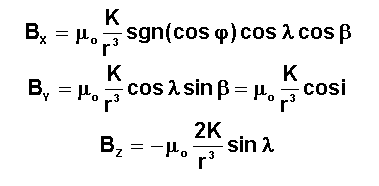
On
observe que dans notre modélisation la composante BY est constante mais
naturellement faible puisque l'inclinaison est voisine de 90° (une orbite
héliosynchrone est presque polaire). Bien sûr avec un modèle plus précis cette
propriété n'est plus vraie et BY a une variation périodique .
4°) MODELE DE CHAMP MAGNETIQUE:
Dans
les simulations servant à valider des concepts de régulation utilisant le champ
magnétique et ( ou ) sa dérivée, l’approche analytique précédente suffit.
Mais
pour un usage et des applications en mission réelle, il faut une connaissance
plus précise du champ magnétique local, fonction de la longitude, de l’altitude
et de l’altitude sol. Des modèles existent, appelé modèles embarqués qui ne
nécessitent qu’une bonne estimation de la position du satellite par rapport à la
Terre.
Vous
trouverez sur ce site une rubrique spécialement destinée au
modèle IGRF (International Geomagnetic Reference Field ) et les
routines utilisables sous Matlab.
III SIMULATION sur un satellite
:
1°) Présentation :
En
1993, un projet avait été lancé, à l'école de l'air, d'étudier un petit
satellite héliosynchrone, en orbite basse à 470 km, pour une mission d'imagerie
spatiale, tolérant une stabilisation sommaire à faible coût financier et
énergétique.
Le
choix avait été fait de stabiliser le satellite par gradient de gravité, avec
après capture, la mise en œuvre d'un amortissement par magnéto-coupleurs
utilisant le champ magnétique terrestre.
La
commande serait donc réalisée au niveau des courants à injecter dans les
bobines, pour générer des couples amortisseurs sur tous les axes.
2°) La simulation :
Elle
porte sur un satellite :
- En orbite basse héliosynchrone d'altitude 437 km
inclinée à 97°.19
- D'inerties roulis Ir = 90 m²kg, tangage It = 120
m²kg, lacet Il = 50 m²kg
- Equipement par 3 magnétocoupleurs à commande
proportionnelle dérivée sur les 3 axes
|
Axe |
Gains /rappel angle |
Gains/ rappel vitesse |
|
Roulis |
kpx
= 25 |
Kdx = 25000 |
|
Tangage |
kpy = 14 |
Kdy = 15000 |
|
Lacet |
kpz = 75 |
Kdz = 50000 |
Ces coefficients sont choisis ici de
manière empirique et demanderaient une étude plus poussée.
- Le champ magnétique est calculée par la routine d'initialisation
SCAODAT.M , le résultat est stocké dans un fichier qu'il faut donner dans
SCADAT2 ( Modification à la main pour le chemin). NB : le chemin actuel est --->
c:\calculer\matlab42\resultat\magneto. Le point de départ du calcul est lors de la traversée
S-N ( Nœud ascendant) de l'équateur.
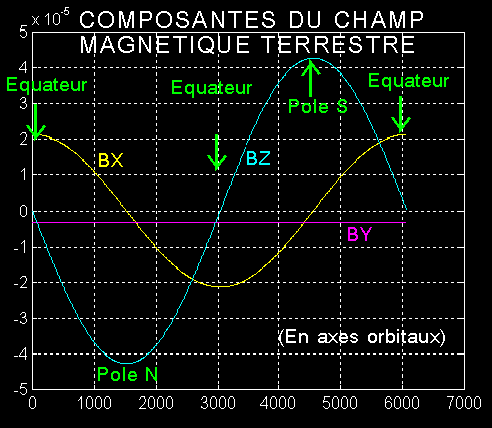
- Les composantes du champ magnétique B sur les
axes XYZ liés à l'orbite circulaire ( X tangent, Y normal portant le
moment cinétique, Z verticale ascendante) sont données, pour information,
sur le graphe suivant, pour une période complète de révolution soit 5599
secondes:
- Un couple perturbateur dû essentiellement à la
traînée sur l'axe tangage peut être introduit grâce à un gain mis à 0 ou
1.
Le
bloc simulation nommé SCAOMAG2.M se présente ainsi :
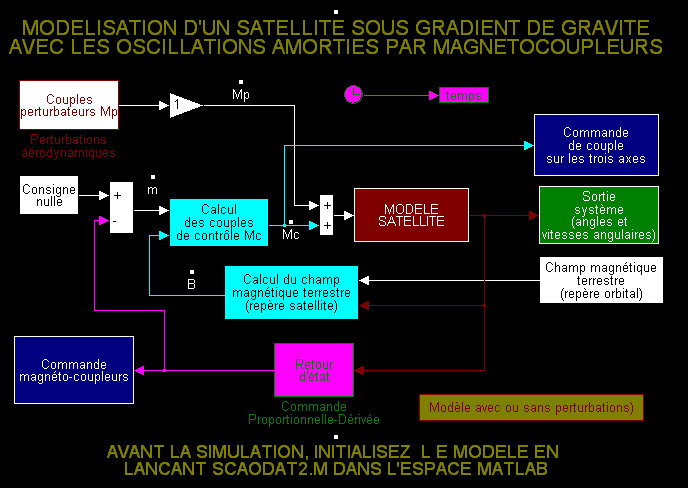
- Le lecteur curieux pourra analyser tous les sous
systèmes et retrouvera les variables intéressantes dans le bloc vert des
angles et de leur dérivées.
NB
1: Il est impératif d'initialiser la simulation en lançant scaodat2.m dans
l'espace de travail Matlab.
NB
2: C'est aussi dans ce fichier que vous pouvez modifier l'orbite et les moments
d'inertie du satellite
NB
3 : Vous pouvez modifier les valeurs des gains dans le bloc rose du retour
d'état, pour en étudier les effets.
3°) Quelques résultats:
a.
En
l'absence de perturbations sur un satellite (Ir = 90 m²kg, tangage It = 120
m²kg, lacet Il = 50 m²kg )
- Sur 6 périodes soit environ 40000 secondes
- Avec des écarts angulaires de 0.1 radian, pour
rester dans le cadre des petits angles
- Sans vitesses initiales
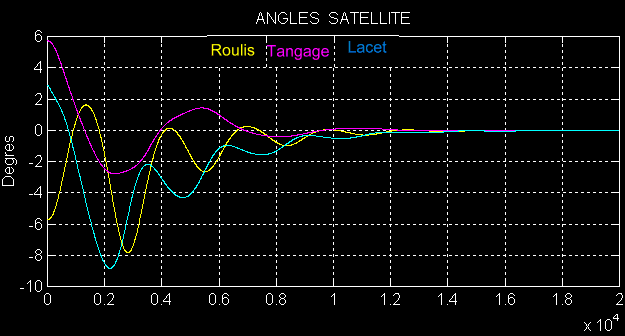
On
note une stabilisation en 4 heure avec retour à zéro de tous les angles.
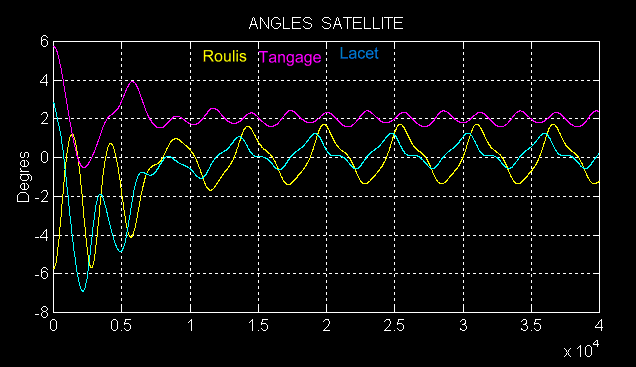
a.
En
présence d'une perturbation aérodynamique donnant un couple de 2 10-5 N-m, sur un
satellite (Ir = 90 m²kg, tangage It = 120 m²kg, lacet Il = 50 m²kg )
Il
apparaît nettement un amortissement sur les 3 angles, avec oscillations autour
de 0 pour le roulis et le lacet, mais autour d'une position décalée pour le
tangage, à cause du couple perturbateur.
Il
est bien connu que les magnétocoupleurs en présence d'une perturbation et à
cause des couplages, ne ramènent pas le système à l'équilibre mais le rapproche
en oscillations de faible amplitude, d'une position résiduelle.
b.
Absence
de perturbation aérodynamique sur un satellite (Ir = 90 m²kg, tangage It = 120 m²kg,
lacet Il = 50 m²kg ), mais diminution des gains sur les vitesses d'un facteur
10
On
constate bien évidemment un amortissement plus lent.
c.
Absence
de perturbation aérodynamique sur un satellite (Ir = 120 m²kg, tangage It = 120 m²kg,
lacet Il = 50 m²kg ), avec les gains initiaux

Avec des moments d'inertie en roulis et tangage égaux, il est impossible en oscillations libres de "contrer" le lacet qui va croître indéfiniment, ce qui déstabilise les autres angles à cause des couplages. Voir Oscillations libres sous gradient de gravité
On
constate aussi que les magnétocoupleurs sont maintenant incapables de
stabiliser le système.
4°) TELECHARGEMENT:
Si
vous désirez récupérer les programmes, vous le pouvez en
"téléchargeant" magnetoc.zip, comprenant:
- Le fichier d'initialisation scaodat2.m
- Le fichier bloc de simulation scamag2.m
- Un fichier pour une fonction de produit
vectoriel dvpnorm.m
- Un fichier de visualisation des résultats
visu2.m
5°) VOIR
UNE APPILCATION TRES COMPLETE A UN NANOSATELLITE:
Ce
site présente une rubrique spécialement destinée à la stabilisation, pointage
zénith, d’un nanosatellite avec utilisation de magnétocoupleurs. Voir les pages dédiées
![]()
Résultat d'une coopération à l'Ecole
de l'Air en 1993
: M Chiavassa (mathématiques) + Cdt Godard (automatique) + M Guiziou (mécanique
spatiale), revu février 1999 et novembre 2001, réactualisé en janvier 2006, et
2012, revu 2014 avec de nouveaux liens