MISSION AMERICAINE STAR DUST

Excellent bureau d'études de 5 h de travail au moins, permettant de "prendre en main" les routines présentes sur le site. Les calculs constituent aussi, pour le professeur, une vérification du projet informatique sur cette sonde.

De façon plus générale, cette étude est une mine d'exercices, pour illustrer les principales notions associées à un voyage interplanétaire.

Première mission interplanétaire avec retour d'échantillons sur Terre

Février 2006, sept 2011

I REFERENCES DES DOCUMENTS :

MEDIA RELATIONS OFFICE
JET PROPULSION LABORATORY
CALIFORNIA INSTITUTE OF TECHNOLOGY
NATIONAL AERONAUTICS AND SPACE ADMINISTRATION
PASADENA, CALIF. 91109.  TELEPHONE (818) 354-5011
http://www.jpl.nasa.gov  & http://stardust.jpl.nasa.gov/news/status/990207.html

I GRANDES LIGNES DE LA MISSION :

TCM = Trajectory Correction Maneuver

ISP = InterStellar Particles

EGA = the Earth Gravity Assist

ACIDA = Cometary and Interstellar Dust Analyzer instrument

1°) LA MISSION :

Source JPL : NASA's Stardust spacecraft successfully shot into a clear blue sky atop a Delta II rocket from Florida's Cape Canaveral Air Station at 4:04:15 p.m. EST (1:04:15 p.m. PST) today to become the first U.S. mission destined for a comet, and the first-ever spacecraft sent to bring a sample of a comet sample back to Earth.

Stardust is on a flight path that will deliver it to Comet Wild-2 (pronounced "Vilt-2" on January 2, 2004. The spacecraft will gather particles flying off the nucleus of the comet. In addition, Stardust will attempt to gather samples from a stream of interstellar dust that flows through the solar system. Captured in a glass foam called aerogel, the comet and interstellar dust samples will be enclosed in a clamshell-like capsule that will be dropped off for reentry into Earth's atmosphere in January 2006. Equipped with parachutes, the capsule will float to a pre-selected spot in the Utah desert, where it will be retrieved and its contents delivered to scientists for detailed analysis.

An orbital design using one Earth gravity assist allows STARDUST to capture cometary dust intact at a low relative speed of 6.1 km/s (as a comparison, Giotto encounter Comet Halley at a relative speed more than 10 times higher). With the aid of onboard optical navigation, the flyby will take place at an encounter distance as close as a 300 kilometers from the comet's nucleus. This extraordinary trajectory imposed a very low post-launch fuel requirement and enabled launch by a Med-Lite version of the Delta II launch vehicle.)

2°) LA TRAJECTOGRAPHIE :

TIR THEORIQUE PREVU LE 6 FEVRIER 1999

Voici d'après le JPL les données concernant l'hyperbole de départ, obtenue après l'arrêt de la combustion du troisième étage.

Dans tous les cas C3 = 26 km²/s²

Date du tir

Déclinaison d

Ascension droite a

6/2/99

- 19°.5

234°.62

12/2/99

-20°.69

240°.69

15/2/99

-16°.02

221°.48

21/2/99

-17°.84

227°.93

Nous adoptons la première occurrence du tir.

C3 = 26 km²/s², déclinaison de - 19°.5 , Ascension droite de 234°.62

Orbites interplanétaires :

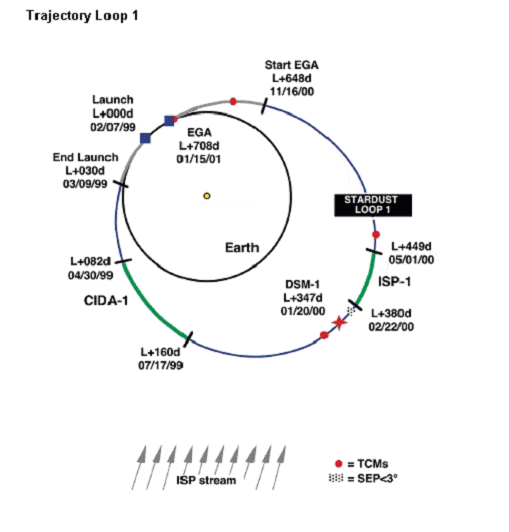
Source JPL : http://stardust.jpl.nasa.gov/mission/details.html The STARDUST spacecraft was launched on February 7, 1999. The first orbital loop was a 2-year path with a 160 m/s delta-V trajectory correction maneuver (TCM) near aphelion. This delta-V set up the Earth swingby that pumped the orbit up to the 2.5-year loop, which the spacecraft flew by twice. At 198 days before encounter, a delta-V of 71 m/s was performed to set up the Comet Wild 2 flyby. This will occur on 2 Jan 2004, at 1.86 AU and 98.5 days past Wild 2 perihelion passage. A 1 AU (Astronomical Unit) test was performed during June-July 2003 to assess the spacecraft performance for Earth return enviroment. The spacecraft will approach the comet at 6.1 km/s from sunside with a 73º phase angle. Coma fly-through will be on the sun side at a planned miss distance of 300 kilometers. Flyby is five years after launch, and Earth return, two years later.

Altogether, three orbits will be made around the sun to minimize the delta-V requirements for the mission so that a Med-Lite version of the Delta II launch vehicle could be utilized. Also, the three orbits will maximize the time for favorable collection of interstellar dust.

 

EPHEMERIDES BDL SUR LA COMETE WILD-2

LE TREMPLIN SUR LA TERRE :

Source JPL : Earth Flyby: January 15, 2001, 1100 Days Since Earth Flyby

Earth closest approach for Stardust occurred on Monday, January 15, 2001, at 11:14.28 UTC (4:14.28 am MST, 3:14.28 am PST). The Stardust spacecraft started the Earth Gravity Assist (EGA) phase of its mission on Tuesday, November 28, 2000, 48 days from closest approach to Earth. On November 28, the spacecraft executed the first of three flight path corrections planned for the EGA phase. The primary objective of the EGA is to provide Stardust with an energy boost from flying past the Earth. The boost, which comes from sling-shoting around the Earth, i.e. a "gravity assist", will increase the spacecraft's orbital period around the Sun from 2 years to 2-1/2 years and alter its flight path to intercept Comet P/Wild-2 on January 2, 2004.

Spacecraft activities are fairly quiescent on approach to Earth, with only engineering housekeeping on the agenda. An attitude maintenance turn was performed on Tuesday, December 5, 2000 to keep the spacecraft's forward-looking medium gain antenna pointed toward the Earth while maintaining adequate sunlight on the spacecraft's power-generating solar arrays. STARDUST successfully completed Trajectory Correction Maneuver #5 (TCM-5) on January 5, 2001, the final targeting for Earth flyby. Five Navigation Camera images were taken to assess camera performance after the 2nd heating sequence where both the CCD and mirror motor heaters were turned on for about 1 month. The spacecraft will then be left alone until after Earth flyby.

Earth closest approach will occur on Monday, January 15, 2001, at approximately 11:20 UTC (4:20 am MST, 3:20 am PST). The spacecraft flies over a point just South-East of the southern tip of Africa, at a distance just over 6,000 kilometers (3,700 miles) from the surface, and a speed of approximately 10 kilometers per second (36,000 kilometers per hour, or 22,400 miles per hour).

Once past Earth, the spacecraft will transfer communications from its medium gain antenna to its aft-looking low gain antennas. Approximately 15 hours after closest approach to Earth, the spacecraft will fly within 98,000 kilometers (61,000 miles) of the Moon.

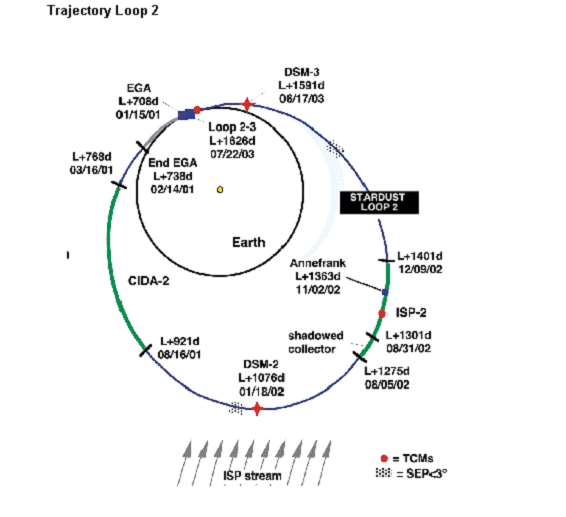
LE GRAND VOYAGE :

Source JPL : Apr 18, 2002 - Since its launch on February 7, 1999, the Stardust spacecraft has traveled over two billion kilometers completing one and a half elliptical orbits around the Sun. On Thursday, April 18th, the mission will reach a major milestone when it arrives at its furthest distance from the Sun, also known as its aphelion.

At this time the spacecraft will be 2.72 Astronomical Units (407 million kilometers or 253 million miles) from the Sun, and near the middle of the asteroid belt. This is the farthest distance ever reached by a solar-powered spacecraft. Far beyond the orbit of Mars, the sunlight intensity is only 13% of what we see at Earth resulting in very cold temperatures and diminished power generation by the spacecraft's solar cells. The spacecraft is performing excellently in this environment and operations teams at the Jet Propulsion Laboratory, California and Lockheed Martin Astronautics, Denver are eager to enter the final phases of the mission.

After aphelion, Stardust will begin falling back towards the Sun and by the end of the mission, in January 2006, it will have completed another loop and a half around the Sun. On January 2, 2004, on its final solar orbit, Stardust will fly past comet Wild 2 to collect samples and return them to Earth in 2006. In January 2006, the samples will be delivered by parachute inside the Stardust Sample Return Capsule to the Utah Testing and Training Range.

LE RETOUR SUR TERRE :

Source JPL : This phase of the STARDUST mission begins two weeks before Earth re-entry and ends when the SRC is transferred to its ground-handling team. The planned landing site is the Utah Test and Training Range (UTTR). Following touchdown, the SRC will be recovered by helicopter or ground vehicles and transported to a staging area at UTTR for retrieval of the sample canister. The canister will then be transported to a dedicated Stardust handling and curation laboratory at Johnson Space Center. The Earth Return is divided into four subphases:

Earth Return Timeline

Time            Event Description 
E - 67 days     Navigation cutoff for TCM at E-60d
E - 60 days     TCM to remove accumulated flight errors
E - 37 days     Navigation cutoff for TCM at E-30d
E - 30 days     TCM to cleanup residual flight errors and set 
                up direction bias for next TCM
E - 19 days     On Low Gain Antenna at similiar Sun-relative 
                attitude as required for SRC Release
E - 13 days     Navigation cutoff for TCM at E-10d
E - 10 days     TCM to perforum preliminary entry
E - 44 hours    Navigation cutoff for TCM at E-1.5d
E - 36 hours    TCM to perform final entry targeting
E - 7.5 hours   Go/No-go Decision for SRC release
E - 4 hours     SRC spin release (spin rate of 14 to 20 rpm)
E - 3.7 hours   Spacecraft divert maneuver 
                (to prevent spacecraft entry)

Earth Approach

Source JPL : Beginning with Earth Approach, the period of near-continuous DSN tracking commences. During this period two TCMs are involved nominally: at ER (Earth reentry) -10 d, ER-36 hr. The SRC will be released at ER-4 hr after the last TCM and will enter the atmosphere at a nominal entry angle of -8.2°. The approach velocity to Earth will be approximately 6.4 km/s with a right ascension of 205.7°, a declination of 11.1°, and velocity at entry (assumed to be at an altitude of 125 km) of 12.8 km/s. The entry corridor control accuracy attainable, based on the Navigation Plan, is 0.08°.
The spacecraft will perform a divert maneuver subsequent to the SRC release to avoid entering the atmosphere.


Entry

Source JPL : Entry begins when the spacecraft reorients for SRC release from the spacecraft bus and ends with parachute deployment. The SRC will be released from the spacecraft bus approximately 4 hours before entry. Significant activities include verifying spacecraft attitude, depassivating the batteries, initiating the SRC on-board timer/sequencer, turning off spacecraft-bus-provided heater power to the SRC, cutting the connecting cable and releasing the SRC.

The SRC will perform a direct entry at Earth. After entry the SRC will continue to free-fall until approximately 3 km, at which point the parachute deployment sequence will initiate. Elapsed time from entry to parachute deploy will be approximately 10 minutes.

 
Terminal Descent - SRC with Parachute

Source JPL : Descent begins when the parachute deployment sequence initiates and continues until the SRC/parachute system has descended into the recovery zone, the UTTR.
The velocity of the SRC must be reduced from the initial entry velocity of 12.8 km/s to a level that permits soft landing.
The aeroshell removes over 99% of the initial kinetic energy of the vehicle to protect the sample canister against the resultant extreme aerodynamic heating. The heatshield is a 60° half-angle blunt cone made of a graphite/epoxy composite covered with a thermal protection system. Ablative material on the backshell protects the lander from the effects of recirculation flow around the entry vehicle.
Taking into account SRC release and entry corridor uncertainties, vehicle aerodynamics uncertainties and atmospheric dispersions, the landing footprint ellipse for the SRC has been determined to be approximately 30 km by 84 km. The SRC will approach the UTTR on a heading of approximately 122° on a north-west to south-east trajectory. Local time of landing will be approximately 3:00 am.

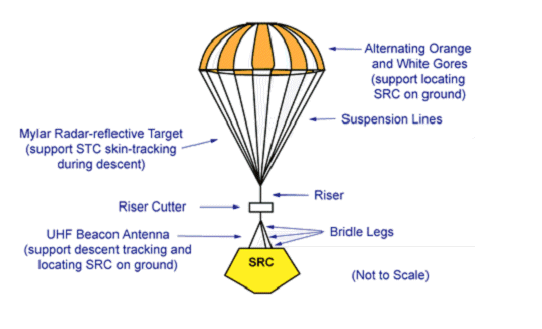
Ground Recovery :

Source JPL : Recovery begins a few hours before the SRC touches down. Retrieval is via ground transportation or helicopter. Given the small size and mass of the SRC, it is not expected that its recovery and transportation will require extraordinary handling measures or hardware other than a specialized handling fixture to cradle the capsule during transport. A gas sample from the canister will be taken for volatile monitoring. Transportation of the SRC to a staging area at the UTTR for packing. The sample return capsule then will be transported to its final destination, the planetary material curatorial facility at Johnson Space Center.


III PROJET

Reconstitution et vérifications de la mission

Vous adoptez un tir du 6 février 1999 (alors que celui de la NASA est du 7/2/99)

DONNEES FOURNIES SUR LE SITE NASA-JPL

Date

Evènement

Valeurs

 

Première correction de trajectoire

Orbite de période T

DV = 160 m/s

2 ans

15/1/2001

Tremplin sur la Terre à 6000 km de la surface

Vitesse au périgée

Période

 

10 km/s

2.5 ans

18/4/2002

Sonde Star Dust à l'aphélie

407 106 km

2/1/2004

Survol de la comète Wild-2

Vitesse d'approche

Angle de phase

 

6.1 km/s

73°

15/1/2006

Retour sur Terre et entrée dans l'atmosphère

Vitesse infinie

Vitesse d'entrée

Ascension droite

Déclinaison

 

6.4 km/s

12.8 km/s

205°.7

11°.1

 

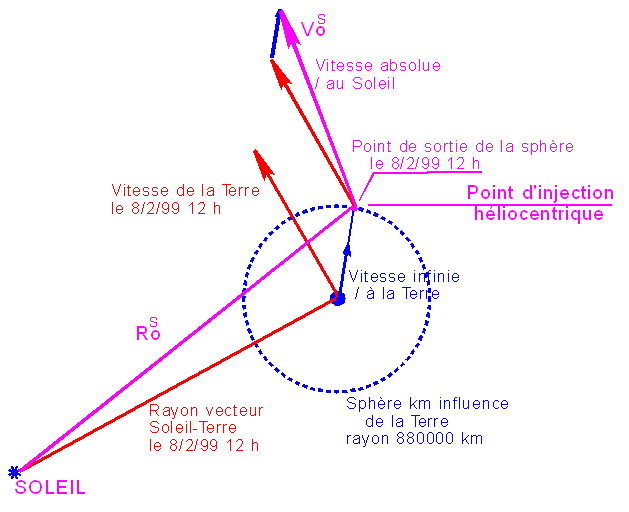
1°) DEPART DE LA TERRE ET INJECTION HELIOCENTRIQUE :

APPROXIMATIONS ADOPTEES : Hypothèse des sphères d'influence éventuellement améliorée - Dates prises à 12 h 0mn 0 s, jusqu'à nouvel ordre - Manœuvres supposées instantanées - Ephémérides avec les routines du site ou celles de IMCCE - Repères J2000

a.     Calculer la durée de la sortie de la sphère d'influence terrestre, supposée de rayon de 880000 km. Vous devriez approximativement trouver 2 jours.

b.     Ce qui donne sensiblement une sortie de la sphère d'influence le 8/2/99 vers 12 h. Vous précisez les éphémérides Terre à cette date.

c.     Vous effectuez le calcul des composantes de la vitesse à l'infini de départ de la terre, par rapport à IJK géocentrique puis XEYEZE héliocentrique.

d.     Vous calculez la position du point d'injection héliocentrique en traduisant la relation correspondant à la figure: Ce qui signifie que vous apportez un peu plus de précision au point d'injection. C'est une approximation meilleure que celle des sphères d'influence réduites à un point.

 

e . Vous calculez les paramètres orbitaux de la première orbite héliocentrique, avant la première correction.

f . Vous en précisez la période, le périgée, les dates importantes et vous commenterez l'intérêt de l'orbite.

2°) PREMIERE CORRECTION DE TRAJECTOIRE :

a) Elle est annoncée par la NASA comme se faisant près du périgée et devant nécessiter environ 160 m/s.

Le but est de rejoindre la Terre le 15 janvier 2001 à 12 h 00 mn 00 s suivant nos conventions de calcul.

La trajectoire modifiée C2 rejoint ces 2 positions, aux dates indiquées. Par la résolution du problème de Lambert, avec DEUX_PTS.EXE en Pascal ou LAMBERTC.EXE en C++, programme que vous pourriez adapter, vous commencez par vérifier ponctuellement que la prévision NASA est bonne. En b) vous affinez le calcul.

b) Vous recherchez ensuite, la CORRECTION OPTIMALE, entre - 100 jours et + 100 jours autour de l'apogée, qui permet de rejoindre la Terre, toujours le 15/1/2001, à coût minimal en propulsion. Pour l'auteur, à titre indicatif, il apparaît que 154 m/s suffisent, alors que vers le 10 février près de l'apogée il faudrait 176 m/s et que la NASA donne 160 m/s mais sans indiquer de date ni de raison pour ce choix.

Par contre, vous devrez vérifier que l'angle Terre-Soleil-Sonde est ou plus grand que 3° ou plus petit que 177°, ceci pour éviter une opposition ou une conjonction avec le Soleil, fatale pour les communications.

c) La correction étant adoptée, vous précisez:

3°) SURVOL DE LA COMETE : :

Au vu des dessins de la NASA, sachant qu'un tremplin n'est jamais vraiment parfait, il vaut mieux, pour l'instant calculer la trajectoire la plus sûre, celle de la fin du voyage, de la comète le 2/1/2004 à la Terre le 15/1/2006.

a.     UTILISATION DE LAMBERTC.EXE :

Vous avez là l'occasion de tester cette routine, pour un voyage interplanétaire à plus moins d'un tour. En effet la sonde Star Dust survole la comète WILD-2 le 2 janvier 2004 à 12 h et rejoint la Terre le 15/1/2006 à 12 h, sur une orbite de période annoncée à 2,5 ans. Commentez le choix de la période de 2.5 années, en pensant à la récupération des poussières de comète.

b.     Donnez pour cette trajectoire de survol:

Retrouvez l'angle de phase, ANGLE ENTRE LA VITESSE RELATIVE ET L'AXE SONDE-SOLEIL, qui servira à orienter la sonde.

IL faut en effet imaginer que la sonde Star Dust est destinée à recueillir des poussières dans la queue de la comète, poussières dont personne ne connaît vraiment bien les dimensions. La vitesse se comptant en km/s, l'énergie cinétique d'un grain de 0.1 g est E=0.5*0.0001*(6000)²= 1800 joules équivalente à une masse de 1 kg à 60 m/s soit 216 km/h, ce qui permet d'imaginer la violence du choc. La rencontre avec une poussière un peu massive est donc hautement dangereuse. C'est la raison pour laquelle, la sonde doit être orientée de manière très précise, avec un bouclier de protection dont l'axe est porté par la vitesse relative.

Vous vérifierez que cet angle vaut bien 73° valeur annoncée par la NASA, au moment du survol le plus proche.

4°) AUTRE CALCUL DU SURVOL DE LA COMETE: :

Dans cette partie, on suppose que la comète est survolée sans correction de trajectoire, grâce au tremplin parfaitement effectué sur la Terre le 15 janvier 2001.

a.     AUTRE UTILISATION DE LAMBERTC.EXE : Nous avons là l'occasion de tester cette routine, pour un voyage interplanétaire à plus d'un tour. En effet la sonde Star Dust survole la Terre le 15/1/2001 à 12 h et doit rejoindre la comète WILD-2 le 2 janvier 2004, sur une orbite de période 2,5 ans, donc en faisant obligatoirement un "tour à vide" avant la rencontre.

La période de 2,5 années permettra à la sonde de ramener les poussières planétaires recueillies, 5 ans exactement après le survol de la Terre le 15 janvier 2001 correspondant à 2 périodes orbitales exactes, ce qui est une prouesse, réalisée pour la première fois par la NASA-JPL.

Donnez alors:

5°) CALCUL DES CONJONCTIONS ET OPPOSITION: :

Ayant calculé les paramètres orbitaux de toutes les trajectoires et les dates de validité de ces orbites, vous êtes en mesure de suivre l'évolution de l'angle Terre - Soleil - Star Dust, pour les conjonctions et les oppositions.

Vous réaliserez un programme de calcul qui permettra de donner toutes les fenêtres où cet angle est soit < 3°, soit > 177°, ceci afin de mettre en place un planning intelligent des télécommunications.

Le tout pourrait être présenté sous forme d'un tableau avec en abscisse le jour julien et en ordonnée soit l'angle soit la distance Terre-Sonde, soit le temps de communication.

6°) RETOUR SUR LA TERRE DU 15/1/2006:

Le 15/1/2006 à 12 h, Star Dust retrouve la Terre, la vitesse d'arrivée à l'infini est la différence des vitesses absolues de la sonde et de la Terre.

a.     Evaluez la vitesse infinie d'arrivée sur la terre à la première orbite.

b.     Calculer la vitesse d'entrée dans les couches atmosphériques à 125 km du sol terrestre.

c.     Retrouver ascension droite et déclinaison de la vitesse à l'infini.

7°) TREMPLIN SUR LA TERRE DU 15/1/2001 :

Proposition d'étude du tremplin:

La vitesse infinie d'arrivée est calculée et connue, avec ici la propriété d'être dans l'écliptique. La NASA indique l'altitude sol Zp du périgée, correspondant à un rayon périgée Rp donné. Ceci fixe l'excentricité e, le demi grand axe a et le demi angle F d'ouverture des asymptotes.

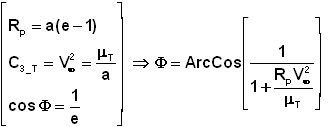
Le lecteur aura compris qu'en fixant le périgée, on fixe la distance du centre attractif de la Terre O à une asymptote

Le problème du tremplin consiste à bien choisir le point d'entrée dans la sphère d'influence, pour obtenir le périgée désiré.

Vu de l'extérieur de la sphère d'influence pour une altitude donnée, il faut viser un point situé sur un cercle de centre O et de rayon Doo, comme le montre le dessin ci-dessous, complétant le précédent:

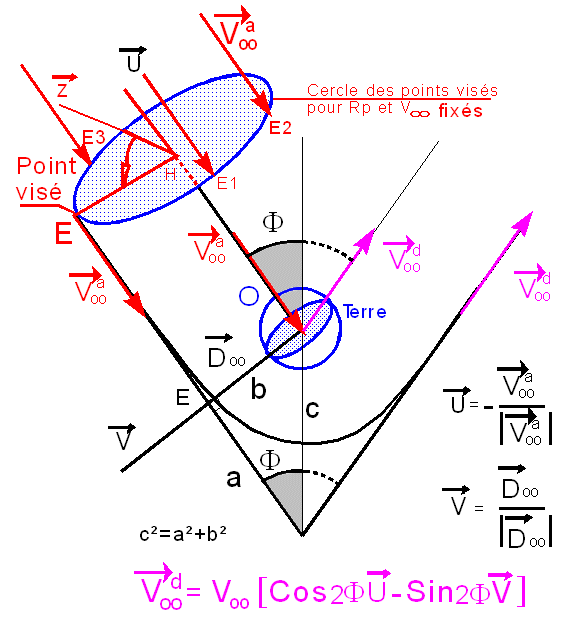
Pour la mission Star Dust, le cercle contient la direction Z du nord écliptique, ce qui permet de repérer le pont d'entrée par un angle y entre Z et HE. La figure illustre le propos.

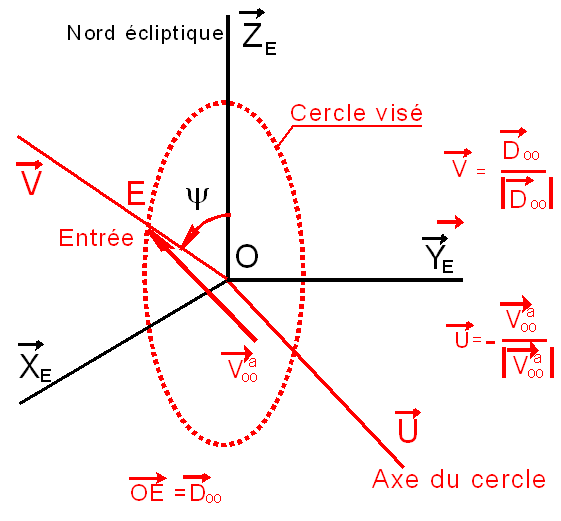
En faisant varier y de 0 à 360°, on balaie toutes les possibilités de survol à Rp fixé. Avec Rp et y on a donc toutes les éventualités pour bien "caler" la vitesse infinie de sortie, en fonction du résultat souhaité, encore faut-il que ce soit possible.

VOTRE TRAVAIL :

1.     Rp fixé : vous effectuez un balayage de y . A chaque valeur, vous calculez :

1.     Vous effectuez un balayage sur l'altitude survol, tout en optimisant le calcul de la correction, à chaque itération et vous tirez l'altitude optimale.

NB : L'auteur a trouvé 13200 km et un DV minimal de 655 m/s. Naturellement il n'a pas tenu compte du petit tremplin effectué en passant près de la Lune, tremplin que vous pouvez commenter.

POUR VERIFIER : Exécuter STARDUST.EXE pour la mission du 6 février 1999.

PROPOSITIONS DE PROGRAMMATION DE L'OPTIMISATION :

1°) REFLEXIONS : L'auteur ne connaît absolument pas les calculs d'optimisation de la NASA.

Ce que nous savons dans ce genre de missions, c'est que la masse de la sonde doit être réduite au maximum. Donc la masse de carburant nécessaires aux corrections de trajectoires et le supplément prévu pour des dispersions inévitables, doit être minimale.

Comme un seul moteur est présent sur la sonde, c'est lui qui assure donc l'ensemble des corrections moteur chaud, c'est à dire importantes.

L'idée que l'on peut retenir est que la somme des incréments de vitesse importants doit être minimale.

2°)  COMMENT ABORDER LE PROBLEME ?

Il paraît évident que le JPL a étudié une optimisation globale de la mission, tant en matière de lanceur, qu'en matière de masse utile. Nous ne pouvons pas prendre en compte le lanceur, sur lequel nous ne connaissons pas les performances.

Par contre, on peut très bien comprendre que le JPL ait choisi une première orbite dans l'écliptique, pour profiter au mieux de la vitesse d'entraînement de la Terre. Par chance ou opportunité, le tir en février est proche du passage de la Terre à son périgée( courant janvier ), la vitesse d'entraînement y est alors maximale, ce qui permet de minimiser la vitesse à l'infini nécessaire. De même le tremplin le 15 janvier coïncide avec un périhélie de la Terre, avec sa vitesse maximale, le choix est donc judicieux.

Nous ne discuterons donc pas le choix de la vitesse infinie ( déclinaison et élévation ) qui conduit à une orbite écliptique. Nous l'appellerons orbite0.

a.     Première correction :

Sur cette orbite, StarDust attend d'être au voisinage de l'aphélie ( normal les corrections de période y sont optimales ), pour délivrer DV1 de l'ordre de 160 m/s pour rejoindre la Terre le 15 janvier.

b.     Optimisation du tremplin :

Elle porte sur 2 variables

1 - Le plan de survol hyperbolique de la terre, qui conditionne la position de la vitesse infinie de sortie. ( Cette optimisation porte sur un balayage angulaire à 1 variable )

2 - L'altitude de survol qui commande l'angle d'ouverture des asymptotes de l'hyperbole et donc aussi la direction de la vitesse infinie. cette optimisation ne porte que sur un paramètre.

c.     Correction en sortie de tremplin :

En sortie de tremplin on obtient une trajectoire qui ne va pas forcément rejoindre WILD2 le 6 janvier 2004. Une deuxième correction de trajectoire est nécessaire et nécessite DV2.

L'optimisation peut donc porter sur DV1 ou DV2 ou DV1+DV2. Cette dernière est la plus compliquée.

3°) RESULTATS POUVANT AIDER L'ETUDIANT :

Seule la mission avec tir le 6 février 1999 et tremplin le 15 janvier a été fouillée par l'auteur avec la mise au point des routines suivantes.

1 - STARDUST.EXE è Programme initial de base comme la NASA avec survol tremplin Terre à 6000 km , avec la simplification des sphères d'influence. Ce programme calcule l'optimisation de DV1 que nous trouvons à 154m/s, donc très près de la valeur NASA et pratiquement à l'apogée puisque l'anomalie excentrique vaut 193°, l'angle Terre-Soleil-Sonde est de 152°. ce qui autorise les communications au moment de la manœuvre. La manœuvre a lieu le15 mars 2000. Comme annoncé par le JPL la nouvelle période avoisine les 2 ans.

Le programme optimise la correction de trajectoire pour rejoindre la comète en balayant toutes les hyperboles possibles de périgée à 6000 km du sol terrestre. La manœuvre DV2 coûte alors un minimum de 440 m/s.

NB :Le seul paramètre sur lequel vous pouvez jouer est l'altitude de survol du tremplin Terre, le 15 janvier 2001..

2 - STRDUST1.EXE è Programme plus élaboré que le précédent, toujours en sphère d'influence simples, mais qui calcule par un double balayage croisé sur la position de l'hyperbole et de son périgée, lors du tremplin Terre le 15/1/2001, le meilleur survol possible.

En pratique, les résultats ( peut-être heureux ) donnent un optimum de survol à 7375 km du sol terrestre ( la NASA donnait 6000 km ) et une correction minime de 45 m/s en sortie de tremplin pour rejoindre WILD2.

 NB : Le programme élimine toute position proche de l'alignement Terre - Sonde - Soleil.

3 - Une idée sur la mise au point d'une optimisation complète : 

 Cet organigramme pourrait se révéler très proche de la réalité :

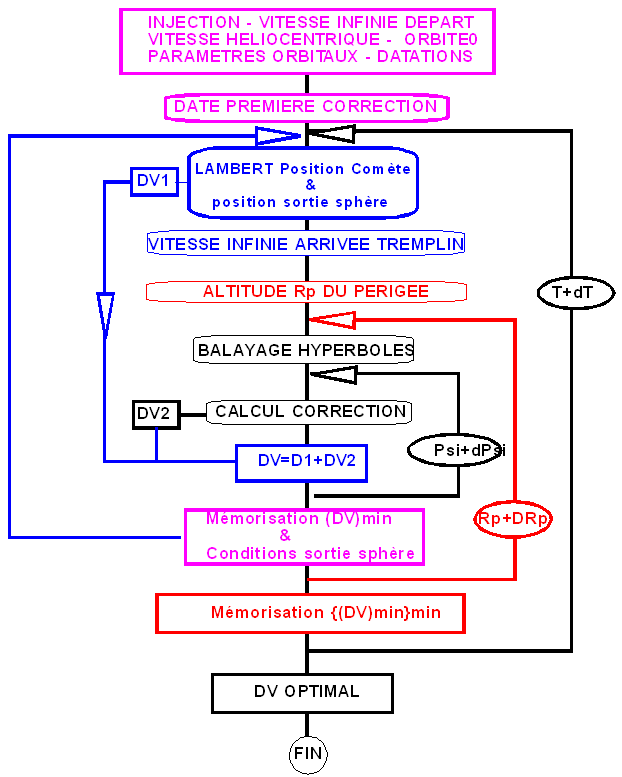
Guiziou Robert janvier 2006, après le retour réussi de la sonde. Rédaction finale en février 2006, sept 2011