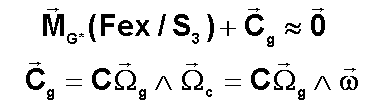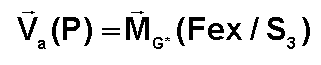|
NOTIONS DE GYROSCOPIE COUPLE GYROSCOPIQUE |
![]()
|
CONTENU : Mis à jour novembre 2000, revu sept
2011 |
|
![]()
Nous
présentons dans les cours qui suivent, les fondements de la gyroscopie. C'est
une partie de la mécanique classique souvent délaissée parce que très
spécialisée, demandant un sens mécanique inhabituel et nécessitant des
approximations, au demeurant fort justifiées mais qui déplaisent quelquefois au
mécanicien trop mathématicien quelquefois.
Les
applications de la gyroscopie et à travers elle des techniques inertielles ont
révolutionné les systèmes de pilotage, de guidage et de navigation parce
qu'offrant une autonomie totale de manœuvre même à des distances considérables
de la Terre ou dans des conditions d'environnement très sévères ( Rentrée de
capsules, sous-marins,...)
1°) CADRE ET HYPOTHESES:
En
pratique, dès qu'un système comporte un corps tournant, on peut parler de
gyroscopie. Cependant l'expérience montre que les effets étonnants et
réellement "utiles" n'apparaissent que dans deux circonstances:
Un
solide unique est en mouvement de rotation, quelle que soit sa rotation, le
mouvement n'est pas alors perturbé par un autre système.
Dans
le cas particulier où le moment des forces extérieures, calculé au centre
d'inertie est nul, l'étude relève alors de la THEORIE DE POINSOT traitée sur ce site.
On
peut alors rappeler qu'en particulier si la rotation axiale se fait autour du
grand axe d'inertie, l'orientation de cet axe reste fixe dans un repère
inertiel. De plus dans le cas d'une grande vitesse de rotation axiale, le
mouvement présente alors une très grande stabilité,
appelée RAIDEUR GYROSCOPIQUE. qui se manifeste par des mouvements très
lents de l'axe du gyroscope, donc des vitesses angulaires très faibles et donc
des accélérations angulaires encore plus faibles.
Nous conserverons cette hypothèse durant tout le cours, elle
sera justifiée à postériori.
Le
corps tournant appartient à un système complexe et présente :
-
Soit un moment d'inertie axial très important
-
Soit une rotation axiale très rapide, par rapport aux rotations possibles des
autres parties du système
-
Soit les deux
Dans
tous les cas on parlera d'un " MOMENT CINETIQUE H
= Iw important", avec une rotation de 250 à 3000 t/s et un moment cinétique de 10-3 à 1
N-m/s
Intuitivement
comparé à la quantité MV qui caractérise l'INERTIE EN TRANSLATION, ici c'est Iw qui
caractérise l'INERTIE EN ROTATION.
2°) HYPOTHESES ET NOTATIONS :
a)
SUR LA FORME DU CORPS TOURNANT( appelé GYRO ) :.
De
toute évidence, il vaut mieux faire tourner un corps de révolution (Toupie)
qu'un solide ayant 3 moments d'inertie différents.
Nous
supposerons donc toujours que le "GYRO" est de révolution axiale,
l'axe de révolution sera toujours noté Z, troisième axe d'un repère principal
XYZ lié ou non au gyro. Le gyro sera noté S3.
|
Matrice
d'inertie du gyro dans le repère principal G XYZ. |
|
b)
SUR LE MONTAGE DU GYRO SUPPOSE ENTRETENU:
On appellera "CARTER"
le solide S2( pourquoi S2, tout simplement parce qu'en général un corps
tournant S3 est monté dans 2 armatures de Cardan, la première dite externe S1
et la deuxième dite interne S2), qui porte le gyro au moyen de 2 paliers A et
A'. Cette dénomination de carter est parfaitement adaptée puisque le gyro doit
être protégé des poussières et régulé en température. De plus la grande vitesse
de rotation présente un danger pour l'environnement extérieur.

Le gyro sera supposé ENTRETENU, ce qui signifie que sa vitesse angulaire de rotation axiale r, par rapport au
carter reste constante dans le temps.
Le CARTER
s'appelle aussi "ELEMENT SENSIBLE",
car c'est lui qui reçoit directement les effets du gyro et lui seul est
vraiment observable. Sa structure sera donc agrémentée d'équipements divers:
-
Moteur d'entraînement du gyro
-
Alimentation électrique de ce moteur
-
Capteur de vitesse angulaire axiale
-
Asservissement de vitesse angulaire.
-
Electronique de l'asservissement.
-
Régulation de température........
-
Paliers A et A',
supposés PARFAITS, c'est à dire sans frottement. Nous n'entrons pas
encore dans le détail de la suspension ( à gaz, magnétique, accordée, roulement
à billes ...).

c)
NOTATIONS :
La
figure ci-dessus illustre les définitions, suivantes :
|
Référentiel
inertiel ou galiléen |
Ra |
|
Centres
d'inertie |
G
pour le gyro G2
pour le carter S2 G*
pour l'ensemble S* = S2 + S3 |
|
Masses |
M
pour S2 M
pour S3 |
|
Vecteur
rotation absolue de S2 |
|
|
Vecteur
rotation de S3/Carter |
|
|
Moment
en P des forces extérieures sur S2+S3 |
|
|
Couple
gyroscopique défini plus loin |
|
|
Rotation
axiale absolue du gyro |
R |
|
Rotation
transversale absolue |
w |
|
Moment
cinétique de S2+S3 |
H |
|
Moment
cinétique de S2+S3=S* , S3 "calé" sur S2. |
H* |
c)
NOTION DE "GYRO CALE SUR LE CARTER" :
Plus
loin, nous serons amenés à utiliser la notion de système avec gyro calé, bloqué
sur son carter. Il s'agira du système global S2+S3, dans lequel le gyro ne
tourne pas par rapport à S3. Autant dire, à paliers "soudés.
Nous
noterons S* ce système particulier, dans lequel le gyro est bloqué sur son
support.
1°) MOMENT CINETIQUE
Soit
P un point quelconque, nous avons :
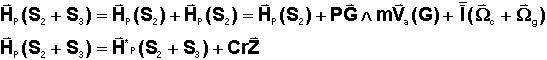
Résultat
évident physiquement.
2°) THEOREME DU MOMENT CINETIQUE:
Appliquons
le théorème du moment cinétique le plus général en P, en remarquant que le
vecteur rZ est constant dans un repère lié à S2.
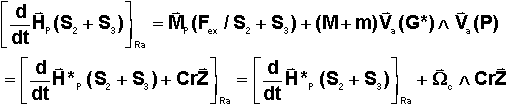
Finalement
on obtient l'équation équivalente ( à * près ):
![]()
3°) NOTION DE COUPLE GYROSCOPIQUE
:
Par
définition, on pose un nouveau vecteur appelé COUPLE
GYROSCOPIQUE :

L'équation
finale de 2°) montre le résultat suivant considéré comme un théorème:
THEOREME TRES GENERAL : EN PRESENCE D'UN GYROSCOPE ON PEUT CONSIDERER
CE GYROSCOPE BLOQUE SUR SON CARTER( Rotation "oubliée" ), A CONDITION
DE RAJOUTER AU MOMENT DES FORCES EXTERIEURES UN MOMENT SUPPLEMENTAIRE , LE
COUPLE GYROSCOPIQUE, compensant les effets de la rotation
"oubliée".
![]()
où
![]()
NB : Le lecteur aura bien remarqué que le mouvement de S2 reste
inchangé, car la mise en équations est strictement équivalente.
4°) INTERPRETATION DU COUPLE GYROSCOPIQUE :
Il
faut essayer ici de faire "sentir" ce qu'est le couple gyroscopique.
Tout d'abord, pour qui a lu la théorie de Poinsot, on constate qu'un grande
moment cinétique pour un solide de révolution totalement libre, crée une très
grande stabilité de ce mouvement. Le meilleur exemple en est la terre dont la rotation reste
immuable avec son axe invariablement pointé vers l'étoile polaire.
On
peut exprimer cette propriété en disant que le gyroscope possède une grande
inertie et qu'il s'oppose à toute action extérieure tendant à lui imposer une
rotation transverse.
Précisément
appelons w le vecteur rotation transverse,
commun à S2 et au gyro S3. C'est le carter S2 qui communique cette rotation à
S3, par l'intermédiaire des paliers.
Le
couple gyroscopique s'écrit donc aussi :
![]()
montrant
qu'il est d'autant plus important que sa vitesse est grande et aussi
proportionnel à l'attaque imposée' w.
Physiquement
et grossièrement, pour créer une rotation transversale w portée par l'unitaire u il faut exercer un couple M
porté par u. Le couple gyroscopique primaire Cg
est alors porté par l'axe v. Mécaniquement il va donc créer une nouvelle
rotation w1 autour de v, donc transversale
aussi.
Que
se passe-t-il alors ? Un couple secondaire Cg1
est crée, porté par l'axe opposé à u, tout simplement pour "contrer"
le couple initial M. Un peu plus loin on montrera et l'expérience le montre
parfaitement, que la première rotation w
est complètement annihilée par cet effet gyroscopique.

Ce
n'est pas simple à imaginer et je le conçois. Mémorisez surtout l'effet
secondaire.
On
pourra cependant retenir une règle simple dite :
4°)
PARADOXE GYROSCOPIQUE :
Nous
sommes en mesure de justifier la dénomination de paradoxe gyroscopique, dans le
comportement "bizarre" d'un gyro.
En
effet la mécanique classique nous dirait qu'un couple M ferait tourner le
solide autour d'un axe sensiblement de même sens que le couple. Or il n'en est
rien, puisque la tendance au parallélisme de l'axe moment et de l'axe de
rotation gyro, montre que la rotation se fait à 90° de celle espérée. C'est lme
PARADOXE GYROSCOPIQUE.
EXPLICATION
: Si maintenant on considère que le le gyro peut être considéré comme
"calé" sur son support, là condition de lui appliquer le couple
gyroscopique, la mécanique classique, appliquée tout à fait normalement à un
solide sans rotation, donne la bonne interprétation, en considérant les
conséquences du couple gyroscopique.
III APPROXIMATION GYROSCOPIQUE :
Considérons
le gyroscope seul.
Hypothèse 1
: Le point de calcul est pris au centre d'inertie G du gyro
Hypothèse 2
: Reprenant l'hypothèse de vitesses angulaires faibles et d'accélérations
angulaires encore plus faibles, on peut négliger les termes provenant de la
dérivée de la rotation transverse.
Hypothèse 3
: Comme les paliers ne peuvent transmettre un moment porté par leur axe Z, le
moment imposé au gyro est transverse
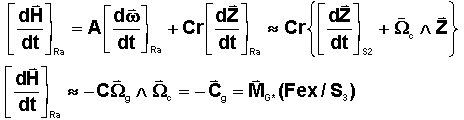
|
THEOREME : Lorsqu'un gyroscope reçoit un
moment, il réagit de manière à créer un couple gyroscopique qui annule ce
moment.
|
Nous
confirmons donc les remarques faites sur le rôle du couple gyroscopique.
Cette
formulation des équations de la gyroscopie est de loin la plus générale :
Indépendante
de tout système d'axes
Indépendante
de tout paramétrage par des angles de rotation.
Très
claire sur le rôle du couple gyroscopique qui "contre" le moment
imposé à S3, transmis par l'intermédiaire des paliers.
FORMULATION EQUIVALENTE :
En
gyroscopie, on s'intéresse essentiellement au mouvement de l'axe gyro, suivi
par des capteurs angulaires qui transformeront plus tard un gyro en détecteur.
On
a donc eu l'idée d'introduire un point P extrémité du moment cinétique
principal H = Cr. Vue de G, la dérivée du moment
cinétique H apparaît comme le vitesse de P.
On
pose donc :
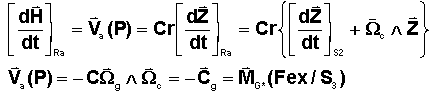
En
conclusion, il vient une relation nouvelle ( attention apparemment il y a un
problème de dimension entre vitesse et moment, mais il ne faut pas oublier que
OP = Cr est un moment cinétique).
|
THEOREME : La vitesse de l'extrémité P du
moment cinétique principal du gyroscope est égale au moment en G des forces
extérieures agissant sur le gyroscope.
|
NB 1 : Cette
approche de la gyroscopie est d'un grand secours pour la description physique
des phénomènes. Elle se prête moins bien aux développements analytiques.
NB 2 : Le
lecteur curieux pourra s'essayer à montrer que l'origine du couple gyroscopique
réside dans les forces d'inertie de Coriolis, dont le moment en G donne
effectivement le couple gyroscopique.
Il
s'agit donc bien d'une forme particulière d'inertie, mais l'origine mystérieuse
des termes de Coriolis, laisse le problème entier.
Pour
créer le couple gyroscopique, le gyro s'impose une rotation transversale w. En gyroscopie instrumentale w s'appelle la DERIVE
ou encore la PRECESSION.
Cette
dérive est tout à la fois :
Une
ennemie quand il s'agit d'utiliser le gyroscope comme moyen de pointage ou de
références d'axes inertiels ( voir Poinsot)
Utile
lorsque, nous le verrons le gyroscope est utilisé comme détecteur, puisque le
couple gyroscopique mettra en évidence des perturbations externes ou des
rotations à mesurer. (Voir instruments de mesure)
Si
l'on remarque que :
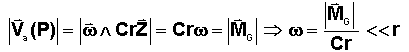
On
prouve à posteriori que plus le moment cinétique H = Cr du gyro est grand, plus
la dérive est faible, on comprend que l'on cherche à atteindre des vitesses de
rotation très élevée, pour réduire la dérive.
Pour
alléger cette page, les exemples nombreux et divers sont fournis à part : VOIR EXEMPLES PRATIQUES.
Nous
ne donnons qu'un seul exemple significatif, car connu de tout le monde : la
toupie.
Une toupie est lancée en rotation de vitesse angulaire ro,
autour de son axe principal Z. Mise en contact, sans frottement, avec une surface
plane horizontale, quel est son mouvement?
On
notera q l'angle de rotation autour de l'axe
u, et y celui autour de l'axe vertical Za.
On note OG = D, M la masse et C l'inertie axiale de la toupie.
Dans
le cadre de la gyroscopie, on peut affirmer que les vitesses et accélérations
angulaires de q et y sont petites. Dans ces conditions l'accélération verticale de G est
quasiment nulle et la réaction N est identique au poids mg.
Typiquement
S* = S2+S3 =Toupie( S2 inexistant).
Le
couple externe M* est porté par l'axe horizontal u et vaut mgDsinq.

a)
RESOLUTION PHYSIQUE :
Si
l'on introduit le point P extrémité su moment cinétique principal, la vitesse
de P est donc portée par l'axe horizontal u, orthogonal à Z. Donc l'angle q ne peut varier, ce qui entraîne que l'axe Z ne peut
avoir qu'un mouvement conique d'axe Za. C'est bien ce qui se passe en pratique.
Si
l'on veut trouver la vitesse angulaire de précession autour de Z, on écrit que
P décrit un cercle de rayon Hsinq.
On obtient alors la précession :
![]()
b)
RESOLUTION CLASSIQUE :
On
s'appuie sur le couple gyroscopique, en posant une vitesse angulaire
transversale w 'dérive ) inconnue :

Pour
conclure simplement comme plus haut :
![]()
NB : Ce résultat
est en partie le résultat moyen du mouvement dit de Lagrange et Poisson, que
vous retrouverez dans tout ouvrage de mécanique classique.
![]()
Guiziou novembre 2000, sept 2011
Il existe une version optimisée pour la mise en page sous Word 97, nommée GYRO_OO.DOC