|
MISSION PHOBOS VERS MARS SOLUTION |
![]()
![]()
PROBLEME
I DE LA TERRE A MARS:
1°) L'exécution de
DEUX_PTS.EXE donne un voyage de 202 jours et les paramètres orbitaux suivants :
La constante C3 de départ de la Terre vaut 11.66 kmē/sē, celle d'arrivée sur la planète Mars 6.91 kmē/sē, correspondant à une vitesse à l'infini d'arrivée sur Mars de 2.63 km/s qui est confirmée par la référence 2 de l'article.
2°) Départ de la Terre :
La conservation de l'énergie sur l'hyperbole donne:
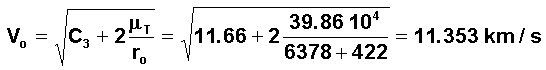
3°) Insertion martienne :
a) La conservation de l'énergie sur l'hyperbole de descente vers Mars donne au périgée, avec un calcul analogue à 2°) une vitesse de 5.212 km/s.
b ) Orbite martienne :
La période de 3 j 5 h 37 mn ou encore 279420 s permet de calculer a = 43992 km. Donc un apogée à 83734 km du centre de Mars, une énergie spécifique E = - 0.4893 kmē/sē et une vitesse au périgée de Vp = 4.3909 km/s.
Ce qui correspond à un freinage
DV = 5212 - 4391 = 821 m/s, très près de la valeur annoncée 815 m/s. Différence normale compte tenu de l'étalement probable de la poussée du moteur. De plus les conditions sont légèrement différentes entre les 2 sondes Phobos I et II.II A PROPOS DE PHOBOS
:1°) Orbite du caillou Phobos :La donnée de la période T = 7 h 39 mn = 27540 s donne un demi grand axe orbital de 9387 km. Réciproquement un demi grand axe de 9377 km donne une période de 27497 s soit 7 h 38 mn 17 s, on peut donc dire que ce sont les arrondis qui font la différence.
2°) a) Estimation de la constante de gravitation de Phobos :
Connaissant sa gravité :1 cm/sē =
m /Rē ===> m = 3.025 105 m3s-2..Compte tenu de la vitesse de libération annoncée à 12 m/s =(.
2m /R )0.5 = 3.96 105 m3s-2Nous en concluons une estimation
m = 3.5 105 m3s-2.b) Estimation de la sphère d'influence de Phobos :
Si D = 9377 km est la distance Mars-Phobos, nous savons que le rayon de la sphère d'influence du "caillou" est alors :
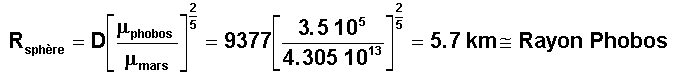
Donc le caillou est tout juste dans sa sphère d'influence, ce qui signifie que près de sa surface les perturbations dues à Mars ne peuvent être négligées et qu'une mise en orbite autour de ce caillou est difficile, voire presque impossible, d'autant plus qu'il n'est pas "rond".
pour une mise en orbite autour de Phobos?
III MANOEUVRES ORBITALES AUTOUR DE MARS :
1°) Manuvre à l'apoastre de C1
:La vitesse à l'apogée de C1 vaut Va1 = 4.391*4250/83734 = 0.223 km/s
La nouvelle orbite C2 a pour diamètre 2a = 83734+9700 = 93434 km, donc une énergie E = - 0.4607 kmē/sē et une vitesse à l'apogée de 0.3267 km/s. L'incrément de vitesse est donc une augmentation de la vitesse de 104 m/s. Valeur analogue et conforme à celle de Phobos II.
2°) Circularisation à 9700 km.
La vitesse d'orbitation circulaire est de 2.107 km/s, celle au périgée de C2 de 2.820 km/s, la circularisation nécessite donc un freinage de 713 m/s. Résultat conforme à l'article, surtout si on pense que probablement un petit ajustement angulaire du plan orbital devait être nécessaire.
3°) Passage sur la même orbite que Phobos.
Pour placer le périgée au niveau de Phobos, a passe de 9700 km à (9700+9377)/2 = 9538.5, donc Da = 161.5 km.
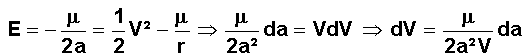
On trouve donc
DV1 = 17.5 m/sUn calcul analogue pour terminer l'opération et circulariser donne
DV2 = 9.1 m/s![]()
Guiziou Robert mars 2002