SOLUTION SUCCINCTE DU CONTRÔLE FINAL
Année 2005/2006
EXERCICE I (10 pts)
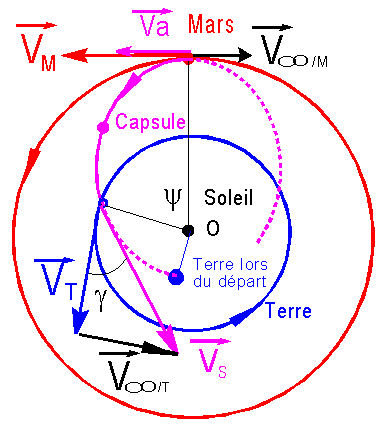
Retour d'une mission interplanetaire martienne:
m
M = 4.305 104 km3/s-2 , RM= 3393 km pour Mars.Terre et Mars sont supposées en orbite circulaire écliptique, de rayon moyen 150 106 km pour la Terre et 228 106 km pour Mars.
Nous sommes en 2020 et une station spatiale a été assemblée à 207 km du sol martien, elle orbite en circulaire, dans un plan confondu avec l'écliptique.

1°) A titre indicatif donner la durée en jours d'un voyage héliocentrique de type Hohmann Mars-Terre?
2a = ( 150+228) 106 km =378 106 km, a = 189 106 km --> Durée = T/2 = 259.35 jours
2°) Ce temps paraît trop long et le problème propose d'étudier la possibilité ou non de revenir en 120 jours. Un calcul
( qui ne peut être réalisé en contrôle et que vous admettez) donne le demi-grand axe a = 148.496 106 km de l'orbite empruntéea) Faire une figure simple ( Orbite de Mars, de la Terre et celle du véhicule
Vérifier qu'effectivement la durée du retour est de 120 jours.
a = 148.496 106 km --> Période = T = 361.25 jours, Ra = a(1+e) ---> e = 0.535395
r = 150 106 = a(1-ecos
j) --> j = 91°.08 = 1.589715 rd![]()
2°) a) Comment doivent être orientées la vitesse infinie de sortie de la sphère d'influence de Mars et la vitesse héliocentrique de Mars, pour optimiser l'opération?
Alignement en sens contraire pour obtenir l'effet de freinage maximumCalculer la vitesse héliocentrique Vs1 au sortir de la sphère d'influence de Mars.
C'est la vitesse à l'apogée sur l'orbite de transfert, l'équation de l'énergie donne VS1 = 16.444 km/s
Déduire alors la vitesse à l'infini de départ ou encore la constante C3M.
Vitesse de Mars en circulaire VM = 24.125 km/s, Vinfini1= VM - VS1=7.681 km/s, c'est une valeur conséquente qui correspond à un C3 = 59 km²/s²
b) Vérifier que l'incrément de vitesse
DV1 qu'il a fallu fournir pour l'évasion martienne à 207 km est de 6878 m/s.La conservation de l'énergie sur l'hyperbole de départ donne la vitesse au périgée de l'hyperbole de départ :

La vitesse circulaire à 207 km est VCM = 3.458 km/s, ce qui entraîne
DV1 = 9.105 - 3.458 = 5.647 km/s3°) Donner l'angle Terre - Soleil - Mars à respecter, au moment du tir au départ de Mars, pour que le rendez-vous avec la Terre puisse se réaliser à la première occurrence après 120 jours de vol.
Avec la valeur de
j = 91°.84 calculée plus haut, et le paramétrage de q, il vient l'angle polaire q![]()
et donc
y = 180° - 124°.03 = 55°.97 et terre doit être en arrière de 360°*120/365.25 = 118°.275 donc l'angle Terre Soleil Mars vaut 118°.275 + 55°.97 = 174°.2454°) QUESTION IMPORTANTE :
a) Calculer la vitesse infinie d'arrivée sur la Terre. Donner alors la constante C3T
Vitesse de la sonde ( avec l'énergie du transfert ) --> VS = 29.59 km/s
Vitesse circulaire de la Terre ---> 29.74 km/s
Pente
g donnée par la loi des aires K = VaRa = VS. ST.cosg --> g = 32°.36 ou encore par K=[ma(1-e²)]^0.5 = 3.749254 109 km²/sLe triangle des vitesses au point de rencontre de la Terre et de la sonde donne :
![]()
ce qui une vitesse très importante avec C3T = 273.35 km²/s².
b) Le retour se termine par une rentrée atmosphérique à 120 km du sol terrestre. Elle doit se faire à 11 km/s, comme pour une cabine Apollo. Vérifier alors qu'un "coup de frein" est nécessaire avec un incrément de vitesse
DV2 = 8900 m/s. Commentaires?Sur l'hyperbole de descente vers la Terre, la conservation de l'énergie donne une vitesse à 120 km de 19.9 km/s, colossale, qui devrait poser d'énormes problèmes de freinage, puisque DV2 = 19.9 - 11 = 8.9 km/s
5°) TREMPLIN INVOLONTAIRE :
(NB : La question 4°a doit avoir été résolue)Imaginons que, suite à un incident, le freinage ne puisse avoir lieu et que la cabine passe au périgée à 150 km frôlant les couches atmosphériques supérieures sans pouvoir rentrer. Un tremplin est alors en cours.
Calculer l'effet tremplin
DV communiqué par la Terre.Il suffit d'appliquer la relation du cours :
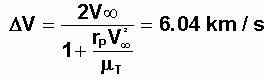
6°) CALCUL DU MOTEUR : NB : indépendante de tout le problème
Calcul de Mp/M, puis Mo/M puis M*/M.
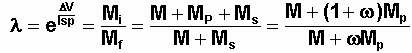
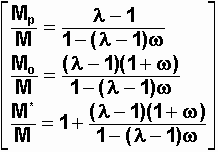
Application numérique
avec une capsule de 5 tonnes. Commentaires.l
= 7.226666, Mp = 16.5017 M = 82.51 tonnes, Mo = 90.76 tonnes, M* = 95.76 tonnes retrouvant ainsi que le rapport de masse est l = 95.76/(95.76-82.51) = 7.2272 c'est à dire aux erreurs d'arrondis près la valeur initiale.
II A PROPOS D'UN SATELLITE GEOSYNCHRONE (5.5 points)
Un satellite géosynchrone équatorial a pour paramètres orbitaux a = 42164 km, e = 0.697467, i = 0°, (
w = 0° W = 270° pour fixer les idées ) , tp = 7/11/2005 14 h 52 mn 24 s1°) a) Vérifier que l'orbite est bien géosynchrone.
T = 86164 s donc identique à celle de la TerreCalculer Rp et Ra les rayons vecteurs à l'apogée et au périgée.
Rp = a(1-e) = 12756 = 2 RT. Ra = 71572 kmb) Placer sur un schéma sensiblement à l'échelle, dans le plan équatorial:
NB vous trouverez des positions bien particulières, ne soyez pas étonnés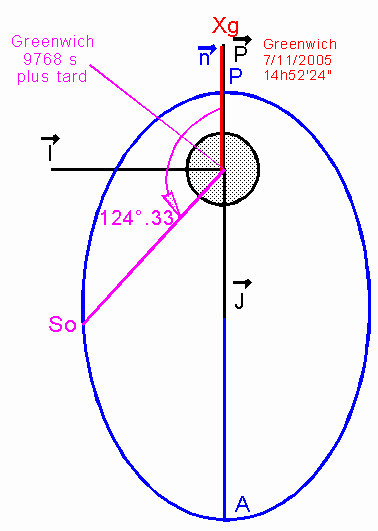
Pour
j = 77°.289 on obtient R =a (1 -ecosj ) = 35693.3 km q = 124°3322°) Pour la position repérée par
j = 77°289 calculer par la loi des aires la vitesse angulaire dq/dt autour de l'axe Nord-Sud et comparer la à la vitesse angulaire de la Terre. Commentaire.La constante des aires vaut K =
ma(1-e²)^0.5= 92902.33 km3s-2 ce qui donne une vitesse angulaire satellite dq/dt = K/R² = 7.29211 rd/s, celle de la Terre est wT = 2p/86164 = 7.29212 rd/s, donc dans le mouvement apparent du satellite par rapport à la Terre, le satellite semble immobile en longitude.Calculer le temps mis depuis le périgée, pour rejoindre cette position So.
Temps de montée 9168 s = 2 h 32 mn 48 sLa longitude Greenwich de ce point s'obtient en retirant de
q l'angle dont a tourné Greenwich durant les 9768 secondes, soit un résultat Lso = q - wT( en °/s)*9168/86164 = 86°.033°) En exploitant les calculs précédents et avec un peu d'imagination caractériser l'ensemble des points survolés par le satellite.
Le satellite est au périgée dans Greenwich, à tp. Pendant 2 h 32 mn 48 s il se déplace vers l'Est plus vite que la Terre et donc survole la longitude 86°.03, qui représente un rebroussement de la trajectoire. Jusqu'à atteindre l'apogée, il va moins vite que la Terre et donc revient vers l'Ouest. Il repasse exactement au-dessus de Greenwich à l'apogée, puisque Terre et satellite, de même période ont tous les 2 fait un demi tour. Le déplacement vers l'Ouest se poursuit jusqu'à atteindre le point de latitude - 86°.03 etc...
Ainsi le satellite survole UN SEGMENT EQUATORIAL ENTRE LES LATITUDES - 86°.03 et + 86°.03
III QUESTIONS DIVERSES INDEPENDANTES (9.5 points)
1°) (0.5 point) A une latitude de 23°.45, sous quel azimut absolu faut-il tirer pour obtenir un plan orbital confondu avec l'écliptique?
L'inclinaison de l'écliptique de 23°.45 nécessite un azimut absolu de 90° ( Tir vers l'Est )2°) (1.5 point) Une manœuvre d'apogée doit relever le périgée 200 km/sol d'une orbite GTO équatoriale, pour le faire passer à 3200 km/sol . Quel est l'incrément de vitesse
DV nécessaire ? GTO --> 2a = 200+6378+42164 = 48742 km , Ra = 42164 km, l'énergie donne Va1 =1.597 km/sCalcul identique avec un périgée à 3200 km : 2A = 51742 km, Va2 = 1.870 km/s donc
DVa = 273 m/sAvec une masse satellite+moteur = 6500 kg, et une Isp = 4400 m/s, il vient
DV = 4400 Ln(6500/(6500-Mp)) soit Mp = 391 kg3°) (1 point) Pour Mars, à 4000 km du centre, quelle est la troisième vitesse cosmique qui permet tout à la fois une libération de Mars et une fois hors sphère d'influence une LIBERATION PAR RAPPORT AU SOLEIL.
Constante de gravitation de Mars 4.305 104 km3s-2, celle du Soleil 13.27 1010 km3s-2.
Le véhicule doit , une fois passée la libération martienne, avoir la libération par rapport au soleil, au niveau de Mars.
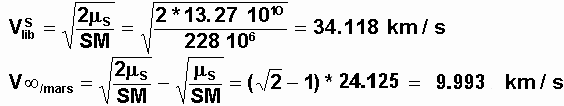
4° ) (3 points) QUESTION IMPORTANTE :
Un tir géocentrique est réalisé avec les conditions de tir absolues suivantes. Rayon vecteur ro = 6578 km, Vitesse absolue Vo = 10.25 km/s, pente absolue
go = 0°, latitude lo = 0°, Longitude Greenwich Lo = 0°, azimut 135°, date 7/11/2005 14 h 52 mn 24 s.Où est le périgée?
Comme la latitude est nulle, le point de tir est sur l'équateur, avec une pente nulle ce point est soit un apogée, soit un périgée, mais comme la vitesse de tir est supérieure à celle d'orbitation circulaire c'est un périgée.Préciser les nœuds.
Les nœuds étant sur l'équateur et le périgée aussi, la ligne des noeuds est lre grand axe avec périgée au noeud descendant ( puisque l'azimut > 90° ),l'apogée est au noeud ascendant.Combien vaut l'argument nodal du périgée
w? Intérêt? w = 0°, plaçant le périgée sur l'équateur et donc l'apogée aussi, excellent pour une circularisation géostationnaire à l'apogée.Pourriez-vous donner un qualificatif à cette orbite?
C'est une GTODonner l'inclinaison orbital.
Cos i = cos lo sinbo = sin 135° ===> i = 45 °Calculer la longitude vernale
W de la ligne des nœuds. W - 180° = Longitude vernale du périgée = Lo +lg(date 7/11/2005 14 h 52 mn 24 s.) = 270° ---> W = 450° (mod 360° ) = 90°5°) (0.5 point) Quelle est la période d'une orbite héliosynchrone inclinée de 98°.7? Commentaire?
Il faut utiliser la relation d'héliosynchronisme
![]()
ce qui donne une altitude sol de 822 km comme SPOT. La période est alors de T =6071 secondes
6°) (2.5 points) NB : Tous les termes de la question sont importants.
Un tir interplanétaire à Z = 422 km du sol terrestre de vitesse relative 11.545 km/s, avec injection plein Est à 23°.5 de latitude, avec la vitesse à l'infini en sens contraire de la vitesse d'entraînement de la Terre( à 150 millions de km du soleil), autour du Soleil. Quel est le périhélie du transfert interplanétaire ainsi obtenu ? Peut-on atteindre Vénus à 108 106 km du Soleil..
La vitesse relative se compose pleinement avec celle d'entraînement de la Terre à 422 km sol, soit Vet ) Vet = 0.455 km/s
La vitesse absolue vaut alors Vo = VR +Vet = 12 km/s
Ce qui annonce une vitesse à l'infini de 5.173 km/s
La Terre orbite autour du Soleil à 29.74 km/s et donc la vitesse absolue par rapport au Soleil vaut VoS = 29.74 - 5.173 = 24.567 km/s
L'orbite héliocentrique a donc une énergie E, un demi grand axe a, une excentricité e et un périgée Rp donnés par
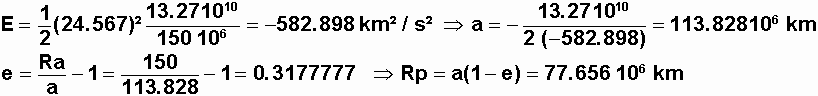 :
:
Comme le périgée est plus proche du Soleil que Vénus, la planète peut être atteinte.