SOLUTION SUCCINCTE DU CONTRÔLE FINAL Année 2003/2004
DESS T.A.E / Mécanique spatiale
EXERCICE I (7 pts)
1°) Quelles sont les vitesses héliocentriques de la Terre et de Vénus?
VT=29.743 km/s, VV=35.053 km/s2°) a) Quelle est la durée du voyage de Hohmann héliocentrique Terre-Vénus?
Durée=146.25 joursb) Donner l'angle Terre - Soleil - Vénus à respecter, au moment du tir au départ de la Terre, pour que le rendez-vous puisse se réaliser à la première occurrence.
Angle Vénus-Soleil-Terre=54°.98 avec la Terre en avance3°) Calculer la vitesse VoT à 622 km du sol terrestre du tir supposé de type Hohmann, profitant au mieux, en sortie de la sphère d'influence terrestre, de l'entraînement de la Terre autour du Soleil.
VOT=10.967 km/s Quelle est la constante C3 du tir? C3=6.39 km²/s²4°) Quelle est la vitesse relative (ou encore vitesse à l'infini d'arrivée ), à proximité de Vénus ( limite sphère d'influence )?
Vinfinie=2.746 km/s5°) Donner la vitesse de survol de Vénus, lorsque la sonde passe au périgée hyperbolique à 200 km du sol de Vénus.
VP=10.558 km/s6°) Calculer le "coup de frein", au périgée, pour passer sur une orbite circulaire à 200 km du sol de Vénus.
DVP=3.349 km/sLa masse totale de la sonde, y compris le moteur, est de 2500 kg. Le moteur utilisé a une impulsion spécifique Isp=4000 m/s, calculer alors la masse Mp d'ergols nécessaires, le calcul devant prendre en compte une marge de sécurité de 100 m/s.
MP=1444.5 kgL'indice de construction est
w=0.125, donner alors la masse restante des équipements scientifiques, une fois le moteur largué. Mf=875 kg________________________________________________
EXERCICE II (8 pts)
Un tir lanceur ARIANE 5 est réalisé dans les conditions suivantes :
* Tir depuis Kourou et surtout
* Orbite finale visée :
Période T exactement égale au tiers de celle de la Terre, pour obtenir un phasage 3/1 avec la Terre. T=28721.3 s=28721 s ===> af=20270.4 km rayon de l'orbite haute* Phase propulsée et injection avec
un azimut relatif bR de 45° et une vitesse relative VR horizontale, pour un transfert vers une orbite circulaire haute, sans changement de plan orbital.NB: le tir n'est pas plein Est et un calcul de composition des vitesses est nécessaire pour reconstituer les paramètres orbitaux absolus.
1°)a) Le point d'injection est-il un point particulier important de l'orbite? Si oui lequel? Nommez-le.
Périgée, car la vitesse relative et celle d'entraînement sont colinéaires et horizontalesb) Que vaut le demi grand axe du transfert? Vérifiez
a=13585 km2°) Donner dans l'ordre qui vous plaira, en vous appuyant sur une figure plane clairement annotée:
a) La vitesse V0 absolue du tir, puis la vitesse relative VR?
b) L'azimut
bo absolu du tir, puis la vitesse relative VR? Vet=435.75 m/s, la relation des sinus donne b0-bR=1°.9, bo=46°.9, VR=8.9174 km/sc) La pente absolue
go et relative gR du tir?( en liaison avec 1°) Pentes nulles, car périgéed) L'inclinaison orbitale i atteinte?
i=50°.78e) L'argument nodal
w du périgée? w=40°.195f) L'excentricité e de l'orbite?
e=0.49213°) Combien de temps après l'injection, le satellite survolera-t-il pour la première fois le point de latitude - 30°?
Une demi période après le périgée soit 7879 s=2 h 11 mn 20 s4°) Question indépendante de tout : Calculer l'incrément de vitesse
DV, nécessaire à l'apogée, après circularisation, pour corriger une erreur d'inclinaison de 0°.1 sur l'orbite circulaire haute à 20270 km de rayon. DV= 7.74 m/s____________________________________________________
EXERCICE III (6 pts)
Ce moteur ionique fonctionnant au Xénon, a une impulsion spécifique Isp=16000 m/s et une poussée F=0.07 Newtons.
La masse initiale de la sonde lunaire est de 365 kg comprenant les équipements scientifiques et le moteur.
1°) Calculer la masse Mp de Xénon à emporter, sachant que la réserve totale de vitesse du moteur est
DV= 3500 m/s. Quelle est la durée Dt totale de fonctionnement du moteur. Mp=71.71 kg, q=F/Isp=4.375 mg/s, Dt=1.6390857 107 s=189.71 jours2°) On admet un fonctionnement en continu, une poussée toujours dans le sens de la vitesse absolue V, et
une orbite initiale circulaire de rayon 18850 km. L'évolution très lente du rayon de l'orbite en continu, permet de supposer qu'à chaque instant l'orbite est quasi circulaire.En utilisant la première des équations de Gauss concernant le demi grand axe a, et après intégration, établir :
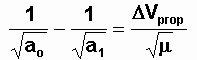
En déduire que les vitesses V0 et V1 sur l'orbite circulaire C0 de départ et d'arrivée C1 vérifient V0 - V1 = DVprop. Evident avec le calcul d'une vitesse en orbite circulaire .
Partant d'une orbite circulaire C0 de 18850 km de rayon, quelle est l'orbite finale C1 obtenue en fin de fonctionnement du moteur? Commentaires en liaison avec la Lune? Vo=4.598 km/s, V1=1.098 km/s, a1= 330342 km. L'orbite finale est en contact à 6000 km près avec la sphère d'influence, la capture par la lune est alors possible.
NB
: Orbite lunaire circulaire de rayon moyen 384000 km, rayon de la sphère d'influence R=60000 km.3°) Question indépendante. Quel aurait été le coût propulsif global, avec un moteur classique, délivrant 2 impulsions pour un transfert de type Hohmann entre les 2 orbites circulaires C0 de rayon 18850 km et C1 de rayon 330822 km. Au périgée Vp=6325.25 m/s, DVp=1727 m/s, à l'apogée Va=361 m/s, Dva=737.5 m/s, DVtotal=2465 m/s, curieusement le coût en vitesse est moindre que par la propulsion continue, mais la suite montrera qu'en masse ce n'est pas le cas.
Avec un bon moteur LH²+LO², Isp=4400 m/s, calculer la masse des ergols nécessaire et la masse scientifique restante une fois le moteur largué. Commentaires, en comparaison avec 1°)?
Mp=156.6 kg, c'est à dire le double de masse d'ergols ce qui diminue d'autant la masse des équipements scientifiques._____________________________________________________
IV QUESTIONS DIVERSES INDEPENDANTES (3.5 pts)
1°) Quelle est la vitesse d'injection au périgée 322 km sol, d'une orbite GTO?
Vp=10.131 km/s2°) Quelle est l'incrément de vitesse nécessaire pour corriger un défaut d'inclinaison de 1°, sur une orbite circulaire à 822 km sol? Où doit-on opérer la correction?
Correction à un des nœuds de 130 m/s3°) Quelle est la vitesse de libération par rapport au Soleil, à une distance de 150 106 km?
VoS=42.063 km/s4°) Quelle est l'inclinaison orbitale d'une orbite héliosynchrone de 422 km d'altitude sol?
I=97°.1115°) Quelle est l'accélération au décollage d'un lanceur de 1000 tonnes, avec des moteurs lui fournissant une poussée totale au sol de 1200 tonnes ( soit 1200 000*9.81 newtons ).
Accélération =F/M-g=1.962 m/s²=0.2 g6°) Pour une injection relative
"plein Est", à une latitude de 35°, quelle est l'inclinaison orbitale atteinte? i=35°7°) Une orbite héliosynchrone d'altitude sol 20000 km est-elle possible?
Non, le calcul de l'inclinaison est impossible, car le |cosi |>1._____________________________________________