|
SOLUTION MISSION ULYSSES |
![]()
![]()
I ETUDE DE LA PREMIERE PHASE
1°) CALCUL DE R ET V :
Le programme donne pour une ANOMALIE VRAIE q = 5°.76854 les résultats suivants :

a) Vérification de a
:Vd = 40.9569 km/s, Rd = 149.43997 106 km
E=V²/2-m/r = -m/2a = - 49.33139 km²/s² donne a= = 1345.114 106 km =1.3451114 109 km , valeur donnée par la NASA à 10000 km près, précision donc extrême.
Période: le calcul classique donne T = 9848.0206 jours
b) Calcul de la date de passage au périgée :
L'équation de paramétrage Rd = a(1-ecosj) donne l'anomalie excentrique de la position j = 1°.396416 = 0.024372 rd.
Le temps correspondant de parcours depuis le périgée vaut alors : 4.237123 jours = 4 j 5 h 41 mn 27.43 s
La date au périgée est donc le 12 octobre 1990 à 13 h 56 mn 51,23 s
c) Avec le vecteur W retrouver la valeur de l'inclinaison orbitale i.
cosi = W.K = W(3) = 0.999396467 ------> i = 1°.9908296 à 0".36 près de la valeur NASA ( Erreurs d'arrondis sûrement )
2°) CALCUL DES DATES JULIENNES :
Le programme donne la date julienne ta = -2924.5 JJ correspondant au 30/12/1991 à 0 h. La date julienne au périgée est -3367.9188542 JJ,
le temps de vol depuis le périgée est donc de 443.4188542 jours solaires moyens de 24 h.Anomalie excentrique à l'arrivée :
Le paramétrage du temps donne 2
p (ta-tp)=T (j - esinj) , la résolution de cette équation transcendante traduite par j =0.88916576sinj + 0.2829079 donne ja = 1.057477 ja = 60°.588986.
3°) UTILISATION DE LA ROUTINE
DEUX_PTS.EXE:NB : Nous ne prenons pas toutes les décimales
Rayon vecteur départ Rd(1)=133.91362 e6 Rd(2)=66.31729 e6 Rd(3)=1.2114 e6 |
Rayon vecteur arrivée Ra(1)= -689.74555e6 Ra(2)= 313.3972e6 Ra(3)= 15.9557e6 |
Résultats pour les vitesses :

Pour les paramètres orbitaux
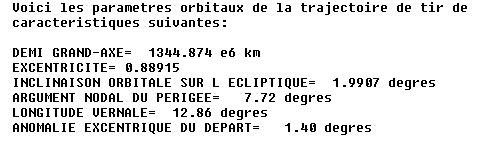
Nous retrouvons avec une excellente et remarquable précision tous les paramètres orbitaux de la NASA.
b) EPHEMERIDES DE JUPITER :
Le programme EPHEMERI donne pour Jupiter:

c) Distance Ulysses-Jupiter :
Un calcul évident de distance donne
D = 50.42 e6 km.Pour ce qui concerne la vitesse relative, elle a comme composantes :
V(Ulysses/Jupiter)=V(Ulysses/Soleil)-V(Jupiter/Soleil)
V(1) = -10.771 km/s, V(2) = 9.535 km/s, V(3) = -0.109 km/s
Sa norme vaut donc
V = 13.87 km/s.d) Sphère d'influence de Jupiter :
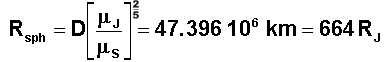
Le calcul permet de vérifier que le 30 décembre 1991, Ulysses se trouve à la limite de la sphère d'influence de Jupiter. Le mouvement devra donc, à compter de ce jour être étudié avec comme seule attraction celle de Jupiter, suivant l'approximation classique des sphères d'influence.
4°)SURVOL HYPERBOLIQUE DE JUPITER:
Un calcul précis aurait donné 38 jours, le calcul approché donne 40 jours
Compte tenu de la notion conventionnelle de sphère d'influence, un temps de 39 jours et un passage au périgée le 8 février 1992, correspondent à une entrée dans la sphère d'influence le
30 décembre 1991 et une sortie le 18 mars 1992. Ces dates confirment l'intervalle de confiance des données.La distance à Jupiter à 38 jours est donnée à 662 Rj.
Le tableau confirme une vitesse à l'infini d'arrivée de 13.87 km/s.
II UTILISATION DES "ROUTINES" ACQUISES
1°) a) Que représente pour vous la date du 19 mars 1992?
Du 8 février 1992 au 19 mars 1992, il s'est écoulé sensiblement 40 jours, Ulysses est donc à la limite de la sphère d'influence de Jupiter et s'apprête à être "prise en main" par le soleil.
b) Quelle est alors la vitesse de Ulysses par rapport à Jupiter?
La lecture du tableau de marche à t=+40 jours après JCA, donnee vitesse de 13.87 km/s, naturellement égale en norme à la vitesse à l'infini d'entrée, conservation de l'énergie hyperbolique oblige.
c) Calculer la vitesse héliocentrique de la sonde Ulysses le 19 mars 1992 à 0 h.
Le calcul demande du soin.
Tout d'abord le 13 mars 95 est le passage au périgée, donc le 19 mars 1992 Ulysses se trouve en train de descendre vers le périgée. Nous devons évaluer le temps écoulé entre ces dates, ceci grâce à DATEJULI:
13 mars 1995 16 h 24 mn 36 s = - 1754.81625 JJ
19 mars 1992 0 h = - 2844.5 JJ
La période est de 2264.4213 jours
La durée est donc de -1089.6838 Jours ou ce qui est équivalent pour le calcul des vitesses, le complément à la période 1174.7375 jours
.La période est de 2264.4213 jours
A ce temps correspond une anomalie excentrique donnée par une équation transcendante :
j
= 0.6026173sinj + 3.0235916 donne j = 3.067936 rd = 175°.78Il faut donc utiliser PAR_RV_S.EXE à la date indiquée ou avec l'anomalie excentrique, ce qui donne pour un temps de 1174.7375 jours, une vitesse absolue:
V(1) = - 0.369 km/s
V(2) = -1.6357 km/s
V(3) = -7.927 km/s
Calculer de même celle de la planète Jupiter
A la même date Jupiter a pour vitesse absolue
V(1) = - 4.395 km/s
V(2) = -11.755 km/s
V(3) = 0.147 km/s
Retrouvez-vous b)?
Ce qui donne une vitesse relative à Jupiter :
VR(1) = 4.358 km/s
VR(2) = 10.119 km/s
VR(3) = 8.074 km/s
Et une norme de 13.66 km/s ce qui correspond bien au tableau de marche vers + 42 j après JCA.
2°) ETUDE DU SURVOL DES PÔLES DU SOLEIL:
sin
lS = sini sin(q+w) où les variables ont une notation classique.a) Quelle est la latitude maximum survolée?
La relation sin
lS = sini sin(q+w) montre que :l
max = i = 79°.109898 et lmin = - i = -79°.109898, qui sont des latitudes très fortes permettant une excellente visée des pôles du soleil.b) Calculer les 2 dates de survol de latitude maximum.
Survol du pôle nord :
lmax = i = 79°.109898, q =p/2 - wdonc avec le paramétrage de
q, on a :cos
q = (cosj-e)/(1+ecosj) qui donne j = 54°.755 = 0.9556562 rd.Le temps depuis le périgée, le 13/3/95 est de 167 jours,
le survol a donc lieu le 27 Août 1995, après le passage périgéeSurvol du pôle Sud :
lmin = - i = -79°.109898Un calcul analogue donne avec
q = - p/2 - w, un survol 152 jours avant le périgée soit le 12 octobre 1994.![]()
Guiziou Robert février2002