RETOMBEE D'UN ETAGE DE LANCEUR
![]()
![]()
On
considère un lanceur, par exemple Ariane 44LP, à l'issue de la combustion du
premier étage , se séparant de son premier moteur qui retombe donc sur terre.
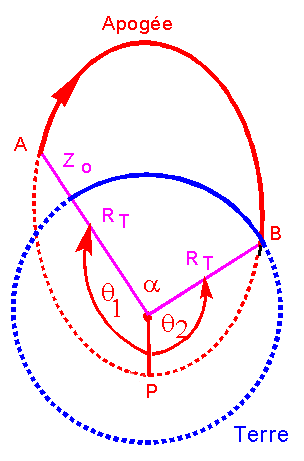 Nous supposons que le vol du lanceur
est situé dans le plan équatorial, avec un azimut de 90°, c'est à dire un tir plein
Est pour profiter au maximum de la vitesse d'entraînement due à la rotation
terrestre.
Nous supposons que le vol du lanceur
est situé dans le plan équatorial, avec un azimut de 90°, c'est à dire un tir plein
Est pour profiter au maximum de la vitesse d'entraînement due à la rotation
terrestre.
On
donne au moment de la séparation du premier étage :
t
= 210 s après le décollage ( à titre indicatif )
Vr
= 2700 m/s vitesse relative par rapport à la Terre
gr = 14°
pente de la vitesse relative sur l'horizontale locale.
Zo
= 60 km altitude au moment de la séparation.
On
rappelle les constantes suivantes :
mT =
39.86 104 km3s-2
RT = 6378 km
T
= 86164 s période sidérale de la Terre.
QUESTIONS
1°)
Calculer la vitesse absolue Vo du premier étage par rapport à des axes
galiléens, non liés à la rotation terrestre. Calculer de même la pente absolue go de la vitesse sur l'horizontale locale.
2°)
Déduire les éléments caractéristiques de la trajectoire képlérienne de retour
vers le sol
a
: demi grand-axe
e
: excentricité
T
: période
Za
: altitude sol de l'apogée de la trajectoire de l'étage.
3°)
Calculer la durée de la phase de retombée en supposant la Terre dépourvue
d'atmosphère.
4°)
Calculer alors la portée angulaire a
indiquée sur la figure. Donner la distance sol parcourue en projection sur le
sol en tenant compte naturellement du rattrapage provoqué par la rotation
terrestre.
![]()
1°) Calcul des conditions absolues de tir.
Dans le plan équatorial terrestre
nous avons la composition des vitesses suivant le schéma suivant .
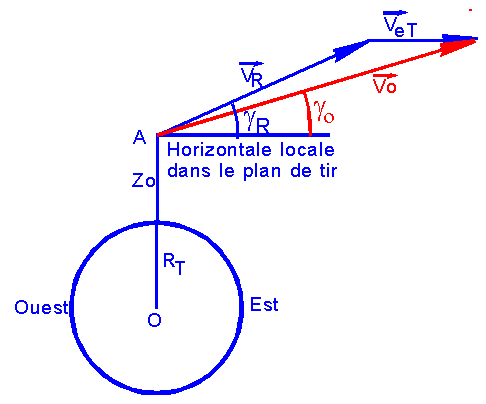
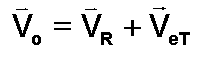
Avec Vet = wT (RT
+ Zo) = 469.5 m/s = 0.4695 km/s
Dans
le triangle hachuré nous avons les relations:
![]()
donnant
Vo= 3157.6 m/s
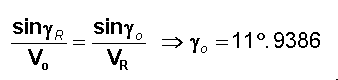
go = 11°.9386
2°) Calcul des éléments caractéristiques de la trajectoire
Nous
calculons les deux constantes caractéristiques E (énergie spécifique) et K
(constante des aires) de la trajectoire képlérienne.
Le
demi grand-axe est a = 3500.9 km
L'excentricité
vaut alors:
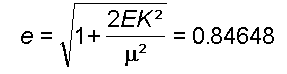
L'apogée
de la trajectoire est Ra = a (1 + e) = 6464.34 soit une altitude Za = 86.34 km
La
période T vaut:
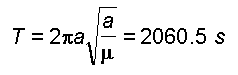
|
e = 0.8465 |
Za = 86 km |
T = 2060 s |
3°)
Calcul du temps de vol avant percussion du sol
Pour
obtenir ce temps de vol il suffit de calculer les deux temps fictifs pour aller
du périgée en A ou en B. Le temps cherché est t = T -t(P->A) - t(P->B).
T(P->A)=
T( jA - e sinjA)/2p où jA vérifie RT = a (1 - e cosjA)
T(P->B)=
T( jB - e sinjB)/2p où jB vérifie RT = a (1 - e cosjB)
Les
calculs donnent sans difficulté:
jA = 172°.435 = 3.00956 rd et jB = 166°.135 = 2.899608 rd
t(P->A)
= 950.4 s et t(P->B) = 884.4 s
Temps de vol: 225 secondes
soit 3 mn 45 s
3°)
Calcul de la portée angulaire :
Les
calculs précédents sont utiles pour évaluer les angles polaires qA et qB
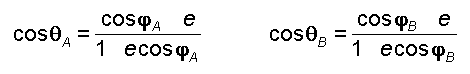
qui
donnent :qA = 177°.815 et qB = 175°.984
La
portée angulaire est a
= 360 - 177.915 -
175°.984 = 6°. 2
a = 0.108227 rd, or pendant 225
secondes la terre a tourné de 0.016407 rd, et finalement la portée angulaire
réelle est de 0.09182 rd, correspondant à une portée au sol de
distance : 585.6 km au sol
Un document du CNES qui relate les diverses séparations confirme
les valeurs calculées.
![]()
Guiziou novembre 1999 et
2005, sept 2011