|
ETUDE DU LANCEUR EUROPA III |
![]()
![]()
L'étude concerne le lanceur Europa 3, prévu pour être construit en coopération européenne. Le projet fut un échec, mais les études d'une motorisation cryogénique ambitieuse du troisième étage, ont été très utiles au développement de la filière Ariane. Europa est l'ancêtre du L3S qui lui aussi n'a pas volé mais a conduit rapidement à la version Ariane 1.
Le premier étage dérivait directement de celui de Diamant, avec un premier étage N204 + UDMH.
Ce problème est excellent pour prendre conscience de l'étagement, de la notion d'optimisation et surtout de l'influence énorme de l'altitude de satellisation sur la masse utile.
PROBLEME
La fiche technique du lanceur est la suivante ne comportant que les données strictement nécessaires au problème.
ETAGE 1 |
Données |
Masse d'ergols ( N204+UDMH ) |
Mp1= 150 t |
Masse de structure |
Ms1= 15 t |
Impulsion spécifique dans le vide |
Isp1 vide = 2717 m/s |
Impulsion spécifique moyenne Temps de combustion |
Isp1 moy = 2630 m/s Tc1 = 150 s |
ETAGE 2 |
|
Masse d'ergols ( LH2+LO2) |
Mp2 =20 t |
Masse de structure |
Ms2 = 3 t |
Impulsion spécifique dans le vide Temps de combustion |
Isp2 vide = 4395 m/s Tc2 = 448 s |
Données annexes et simplifications
:1 - La coiffe, de masse MC = 1.4 t, qui normalement est larguée en cours de fonctionnement de l'étage 2, est supposée larguée en fin d'étage 1, exactement comme Ms1.
2 - L'impulsion spécifique de l'étage 1 sera prise constante et égale à la valeur moyenne.
3 - La masse utile sous coiffe est notée Mu.
4 - La somme totale des pertes pour une mission d'orbitation circulaire à une altitude Z, est donnée dans le tableau suivant :
Altitude Z en km |
D Vpertes = f(Z) en m/s |
200 |
1700 |
300 |
1915 |
400 |
2200 |
500 |
2535 |
600 |
2900 |
700 |
3320 |
800 |
3800 |
I CALCUL DES PERFORMANCES PROPULSIVES
1°) Donner l'expression littérale numérique, avec les masses en tonnes, des performances propulsives
DVprop du lanceur complet, en fonction de la seule variable Mu.On établira un tableau avec en détail
DV1, DV2 délivrés par les 2 étages, et DVprop = DV1 + DV2 = g(Mu), pour Mu variant de 0 et 6 tonnes, par pas de 0.5 tonnes. On pourra éventuellement tracer un graphe.2°) COMMENTAIRES :
a) Comparer en pourcentage la variation de masse lanceur au décollage( pour Mu=0 et Mu=6 t), corrélativement à la variation en pourcentage des performances propulsives.
b) Comparer également la sensibilité à Mu des incréments de vitesse
DV1 et DV2, on calculera la dérivée de DVprop par rapport à Mu en m/s/kg, pour une mission où Mu = 3500 kg.c) Déduire alors grossièrement une estimation du gain de masse utile généré par la rotation terrestre à l'équateur, pour un tir utilisant au maximum cet "effet de fronde" d'environ 480 m/s.
II CALCUL DES PERFORMANCES EN MASSE UTILE
Dans tous les cas seules des missions de mise en orbite circulaire sont envisagées. On souhaite confirmer le résultat de 2°) c) et calculer la masse utile satellisable à une altitude sol Z ( en km ), entre 200 et 800 km.
Plusieurs cas sont envisagés.
1°) TIR EN TERRE IMMOBILE :
2°) TIR EQUATORIAL "PLEIN EST",en terre mobile :
3°) TIR "PLEIN EST" à partir d'une base de latitude 28°:
Dans chaque cas on dressera le tableau des masses utiles Mu satellisables à l'altitude Z et on commentera les résultats.
III CALCULS D'AVANT PROJET
MASSE UTILE GARANTIE EN ORBITE A 200 km
Revenons dans la technique de l'époque, et imaginons nous au stade de l'avant projet d'étude de faisabilité du lanceur. Les ingénieurs disposent des données techniques bien définies du moment, mais travaillent sur un projet dont le développement prendra peut-être 8 à 10 ans, années durant lesquelles des progrès technologiques certains seront réalisés.
Les caractéristiques choisies ont donc des valeurs projetées, entachées d'une dispersion pessimiste possible.
Exemples :
Ces écarts pénalisent donc le lanceur. L'idée est alors de dire que ce sont de petits écarts qui ne changent en rien la mission( pertes inchangées, altitude inchangée, loi de montée identique ). Seule la masse utile sera diminuée, toutes choses restant égales par ailleurs.
On partira donc de l'expression de DVprop, fonction de 8 variables et on opérera un calcul différentiel à bilan global nul dDVprop=0.
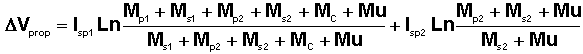
MISSION CHOISIE
: ORBITATION CIRCULAIRE EQUATORIALE A 200 KM.1°) Calculer les valeurs numériques des 8 dérivées partielles de
Dvprop par rapport aux 8 variables ( masses ou Isp) apparaissant dans son expression.2°) Déduire alors la masse utile minimale garantie en circulaire à 200 km.
3°) Le lanceur est maintenant éprouvé depuis plusieurs vols et des besoins nouveaux se font sentir avec une demande d'augmentation des charges utiles en orbite. Faut-il changer de lanceur ou améliorer celui existant? On envisage donc d'abord la deuxième solution en travaillant sur l'étage 2, dont on augmentera la masse des ergols.
Technologiquement, une augmentation de la masse d'ergols de
DMp2 s'accompagne d'une modification des réservoirs et donc d'un surcroît DMs2 = 0.06 DMp2 de structure. On admettra que l'étage 1 reste inchangé tant que l'augmentation totale de masse ne dépasse pas 2000 kg.Quel serait alors le gain maximal de masse utile envisageable en acceptant cette contrainte des 2000 kg max?
![]()
![]()
I PERFORMANCES PROPULSIVES :
1°) Expression littérale numérique des performances propulsives en fonction de Mu.
Le lecteur s'appuiera sur la cours pour établir :
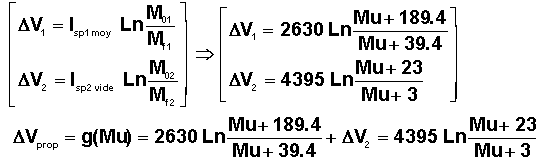
Une programmation sommaire conduit au tableau des résultats suivants :
Mu en tonnes |
D V1 (m/s) |
D V2(m/s) |
D Vprop(m/s) |
0 |
4129 |
8952 |
13081 |
0.5 |
4103 |
8369 |
12472 |
1 |
4077 |
7875 |
11952 |
1.5 |
4052 |
7447 |
11499 |
2 |
4027 |
7074 |
11101 |
2.5 |
4002 |
6742 |
10744 |
3 |
3978 |
6445 |
10422 |
3.5 |
3954 |
6176 |
10130 |
4 |
3930 |
5933 |
9863 |
4.5 |
3907 |
5710 |
9617 |
5 |
3884 |
5506 |
9390 |
5.5 |
3861 |
5317 |
9178 |
6 |
3839 |
5142 |
8981 |
2°) COMMENTAIRES :
a) Le calcul montre de manière frappante qu'une variation de 6 tonnes sur une masse à vide de 189.4 tonnes, soit une variation de 3.17% de la masse au décollage, provoque un "effondrement" de 4100 m/s sur la performance maximale à vide de 13081 m/s, ce qui représente une diminution de 31.34 %. On en déduit donc l'extrême sensibilité des performances par rapport à la charge utile. Ceci explique l'utilisation de technologies de pointe et la recherche d'équipements de masse optimisée, dans l'industrie spatiale.
b) Un examen détaillé montre que l'étage 1 beaucoup plus massif, est beaucoup moins sensible ( 7% de pertes ) que l'étage 2, plus léger ( 42.6 % de pertes ). C'est une remarque qui peut aisément se généraliser à tous les lanceurs multiétages.
Le calcul de la dérivée de la fonction f(Mu) par rapport à Mu ou celui de la pente du graphe associé donne:
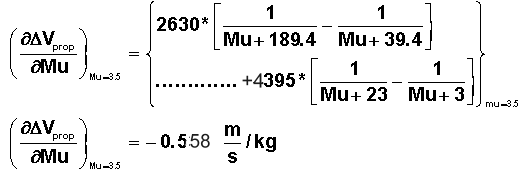
Autant dire que tout kg supplémentaire de masse utile coûte 0.5 m/s de vitesse propulsive.
Donc si la rotation de la terre apporte sensiblement un gain de vitesse de l'ordre de 480 m/s pour un tir équatorial ( cas de nos lanceurs de type Ariane et de la base de Kourou ), on peut en déduire avec une bonne approximation que le gain de masse utile est de l'ordre de 1000 kg. C'est considérable et c'est ce qui a donné beaucoup à réfléchir à l'industrie spatiale soviétique.
II PERFORMANCES EN MASSE UTILE :
Dans tous les cas la résolution de la question repose sur les points importants suivants:
a) Le cours qui indique:
![]()
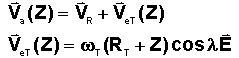
Donc :
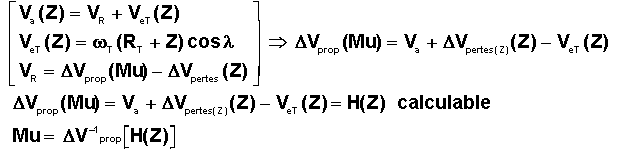
Connaissant
Dvprop, L'inversion conduisant à Mu, peut se faire soit par itération, soit recherche de zéro, soit tout simplement par interpolation sur le graphe des performances, s'il a été tracé.1°)TIR THEORIQUE EN TERRE IMMOBILE :
A l'évidence, la direction du tir et la latitude de l'injection n'ont aucune importance sur la performance du lanceur.
Z |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
Va(Z) |
7784 |
7726 |
7669 |
7612 |
7558 |
7504 |
7452 |
D Vpertes |
1700 |
1915 |
2200 |
2535 |
2900 |
3320 |
3800 |
Vet(Z) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
D Vprop |
9484 |
9641 |
9869 |
10148 |
10458 |
10824 |
11252 |
Mu (kg) |
4787 |
4450 |
3990 |
3468 |
2942 |
2382 |
1803 |
1°)TIR REEL EN TERRE MOBILE :
A l'évidence, la latitude d'injection ( dans le plan équatorial ici) a une importance. Ces tirs profitent au maximum de l'entraînement dû à la rotation terrestre.
Z |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
Va(Z) |
7784 |
7726 |
7669 |
7612 |
7558 |
7504 |
7452 |
D Vpertes |
1700 |
1915 |
2200 |
2535 |
2900 |
3320 |
3800 |
Vet(Z) |
480 |
487 |
494 |
502 |
509 |
516 |
523 |
D Vprop |
9004 |
9154 |
9375 |
9645 |
9949 |
10308 |
10729 |
Mu (kg) |
5938 |
5560 |
5036 |
4439 |
3834 |
3190 |
2523 |
On observe que le gain de masse utile varie de 702 à 1151 kg. Pour les orbites basses, l'estimation de 1000 kg était correcte.
1°)TIR REEL EN TERRE MOBILE, A UNE LATITUDE DE 28° :
Ces tirs sont pénalisés par une baisse de la vitesse d'entraînement de la Terre.
Z |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
Va(Z) |
7784 |
7726 |
7669 |
7612 |
7558 |
7504 |
7452 |
D Vpertes |
1700 |
1915 |
2200 |
2535 |
2900 |
3320 |
3800 |
Vet(Z) |
424 |
430 |
436 |
443 |
449 |
456 |
462 |
D Vprop |
9060 |
9211 |
9433 |
9704 |
10009 |
10368 |
10790 |
Mu (kg) |
5794 |
5420 |
4904 |
4316 |
3721 |
3089 |
2433 |
La pénalité est modeste, variant de 90 kg à 144 kg.
III CALCULS D'AVANT PROJET
Pour Z = 200 km et donc une masse utile de 5940 kg, le lecteur vérifiera les valeurs qui suivent :
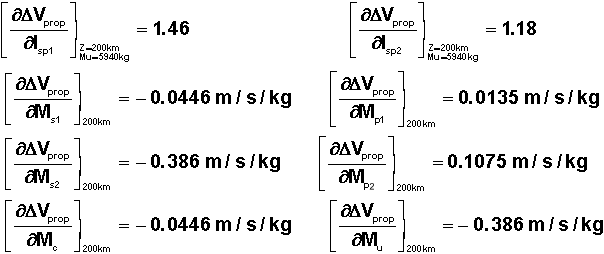
2°) MASSE UTILE GARANTIE A 200 KM :
On note
Dmu inconnue la variation de masse utile compensant les autres dispersions maximales connues :D
ms1 = Dw1*Mp1 =0.005*150000 = 750 kgD
ms2 = Dw2*Mp2 =0.01*20000 = 200 kgD
Isp1 = -20 m/s et DIsp2 = -25 m/sD
mc = 50 kgLe calcul différentiel donne :
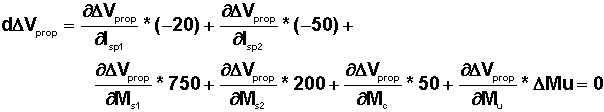
Numériquement la pénalité est
Dmu = - 521 kgLa masse garantie en orbite est donc de 5418 kg
3°) AMELIORATION DE L'ETAGE 2 :
Ecrivant que les performances restent inchangées sous l'effet des variations de Mp2, Ms2, Mu, on obtient :
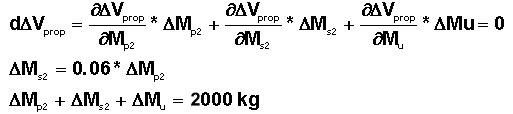
La résolution des 3 équations linéaires donne un
gain de masse utile de 341 kg avec 1565 kg supplémentaires d'ergols et 94 kg de structure en plus sur le deuxième étage.![]()
GUIZIOU Robert novembre 2002
Une version Word 97 existe optimisée pour la mise en page, nommée
Europa_3.doc