POINTS SURVOLES

	Mise à jour septembre 2002, revu sept 2011 I Hypothèses préliminaires Repères et notations Matrices de passage II Méthode de calcul de la trace III Etude de la trace Expression de la latitude Exploitation pratique des résultats Notion de phasage képlérien Phasage non képlérien IV Autre méthode du calcul de la trace V Logiciel de simulation de traces

Ce chapitre est consacré à l'étude de la trace au sol d'un satellite et de son mode de calcul.

On pressent bien que le calcul de la latitude ne devrait pas poser de problème, parce que la rotation terrestre n'intervient pas. Par contre pour la longitude, il n'en sera pas de même.

La connaissance de la trace au sol et de l'instant de survol est indispensable dans l'exploitation des données satellitaires par exemple en:

o Imagerie et cartographie spatiale (SPOT, HELIOS)

o Météorologie ( METEOSAT en géostationnaire , et d'autres en orbite polaire.)

o Télécommunications ( radio, télévision, télécommande et télémesure ) EUTELSAT, TELECOM 2A 2B 2C,

o Contrôle aérien ou maritime ( MARECS,…)

o Sécurité en mer (Système ARGOS )

o Etude des océans (TOPEX-POSEIDON )

o Géodésie spatiale

I HYPOTHESES ET CALCULS :

Une mission satellite est parfaitement définie par ses paramètres orbitaux, ce qui équivaut naturellement à la donnée des paramètres d'injection ( voir PARAMETRES D'INJECTION ou PARAMETRES ORBITAUX )

On supposera donc connus les paramètres orbitaux a, e, i, w, W, tp et l'instant courant t. Nous devons alors calculer la position du satellite par rapport à la terre, par ses coordonnées géographiques longitude L_S et latitude l_S.

Les perturbations orbitales ne seront pas prises en compte dans l'étude initiale, nous travaillons en képlérien, mais nous verrons que les résultats peuvent être extrapolés au cas du mouvement réel.

1°) REPERES ET NOTATIONS:

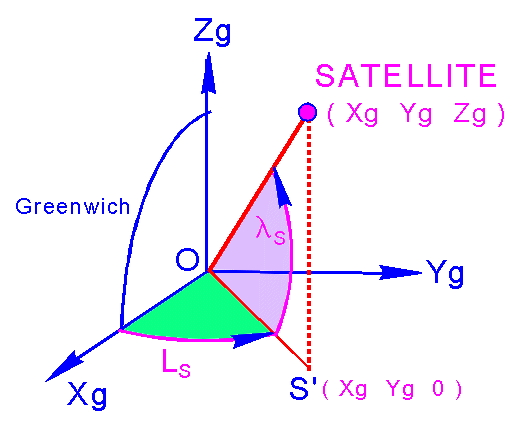
o IJK désigne le repère inertiel Ra, associé à J2000.

o XgYgZg ( Zg=K ) est le repère Rg lié à la terre, en rotation autour de l'axe nord-sud, avec Xg dans le méridien de Greenwich. LS et lS sont rapportées à ce repère. Le satellite S a pour coordonnées Xg, Yg, Zg

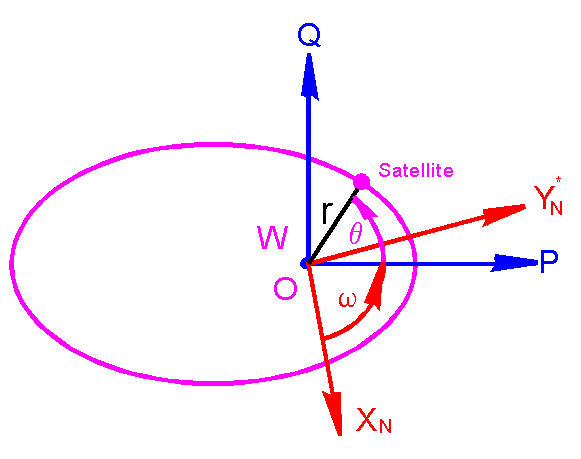
o PQW est le repère périfocal déjà rencontré, associé à l'orbite, avec P pointé vers le périgée et W unitaire du moment cinétique.

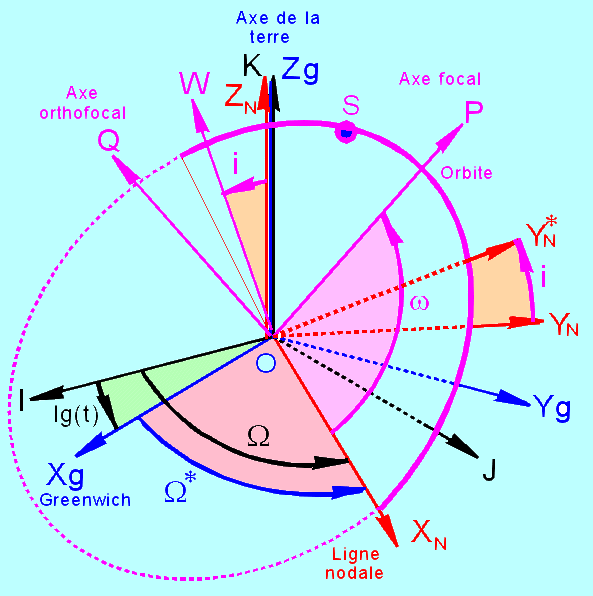
W* = W - lg(t) est la longitude Greenwich de la ligne des nœuds au temps t. On rappelle que lg(t) est l'heure sidérale de Greenwich, calculable par la routine heur-sid.exe ou donnée par les éphémérides du bureau des longitudes.

2°) MATRICES DE PASSAGE :

Nous verrons plus loin que le satellite est facilement repérable dans la base périfocale, et que nous devrons le positionner dans XgYgZg. La matrice de passage est donc nécessaire. Un calcul analogue a déjà été réalisé, dans lequel il suffit simplement de changer W en W*.

_o Passage XgYgZg (Zg=K) à X_NY_N Z_N (ZN=K) : la rotation d'angle W* autour de K permet ce passage, de matrice associée P₁

_o Passage X_NY_NZ_N à X_NY*_NW : la rotation d'angle i autour de X_N permet ce passage, de matrice associée P₂

_o Passage X_NY*_NW à PQW : la rotation d'angle w autour de W permet ce passage, de matrice associée P₃

Ce qui donne en détail les matrices :

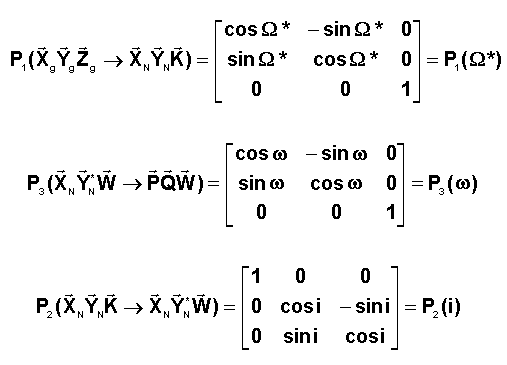
La matrice de passage cherchée est : P = P₁(W*)P₂(i)P₃(w)

II METHODE DE CALCUL :

Les paramètres orbitaux sont connus a, e, i, W , w, tp ainsi que l'instant t. Nous donnons ci-dessous l'organigramme de calcul.

• 1- La donnée de l'instant t permet de calculer, au point courant, la valeur de l'anomalie excentrique j de manière unique

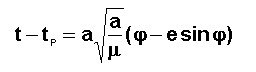
NOTE DE CALCUL :L 'équation étant transcendante la meilleure méthode consiste à calculer j par itération, en partant d'une valeur quelconque jo , et d'utiliser la relation ci dessous :

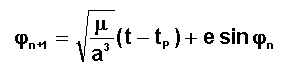
La convergence est assurée et assez rapide vers la solution unique.

· 2- On calcule les coordonnées du satellite dans la base PQW par:

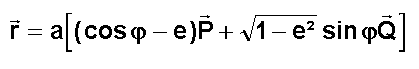
et donc

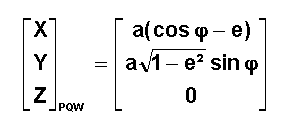
· On effectue le changement de base, qui donne les coordonnées dans le repère de Greenwich

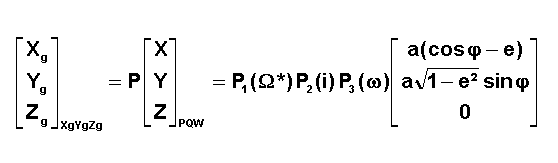
· On en déduit les coordonnées géographiques L_S et l_S.

III ETUDE DE LA TRACE :

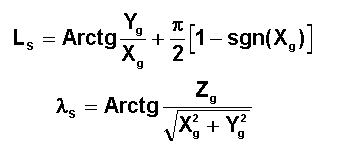
1°) Formule explicite donnant la latitude :

Les calculs précédents sont particulièrement obtus et ne permettent pas d'appréhender la forme de la trajectoire d'un satellite.

Si on revient au repère XgYgZg, on peut écrire Zg = r sinl_S, et en revenant à la base X_NY*_N W, on a aussi la relation

La combinaison des 2 relations fournit une relation très importante en pratique

2°) Exploitation du résultat :

· Sur la trajectoire l'anomalie vraie varie de à 2p, pour une orbite complète. Donc la latitude oscille entre +i et -i. En particulier lorsqu'on souhaite pouvoir survoler une latitude donnée, il faut choisir une inclinaison orbitale supérieure ou égale à cette latitude.

_· Nous avions déjà vu que lors du lancement la latitude de l'injection et l'azimut du tir définissaient complètement l'inclinaison orbitale par cosi = cosl_osinb_o

· On peut donc en déduire qu'avec une inclinaison orbitale élevée, il faudra ou injecter à une latitude élevée en profitant de la rotation terrestre dégradée à une latitude forte, ou garder une latitude moyenne et choisir un azimut proche de 0, empêchant donc de profiter pleinement de la rotation terrestre. Dans les 2 cas le tir est pénalisé. La recherche d'une inclinaison orbitale élevée est pénalisante en masse utile.

· On peut pour les orbites basses faiblement excentriques donner l'allure d'une trace correspondant à une période.

En effet, sur orbite basse quasi circulaire la vitesse angulaire satellite est environ 15 fois celle de la terre. Donc le satellite se déplace rapidement et en continu vers l'Est, de plus en latitude il oscille entre +i et -i. La combinaison des deux mouvements va donner à la trace, la forme approximative d'une sinusoïde.

La trace a donc l'allure ci-dessous, pour un satellite injecté à Lo=20°, lo=45°, bo=45°, sur une orbite circulaire type navette US à 280 km du sol terrestre. L'inclinaison orbitale est i = 60°, la période T= 1 h 30 mn 7 s.

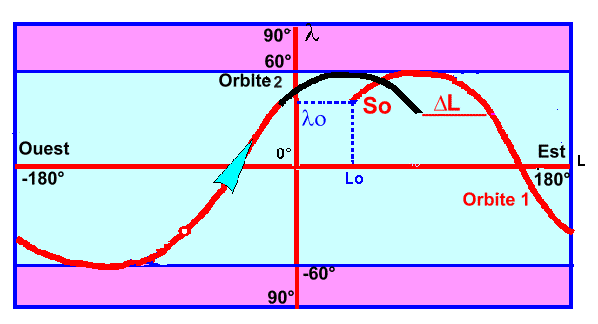
 On remarque alors très simplement que la trace de l' orbite i+1 se déduit de celle de l'orbite i par une translation vers l'Ouest de DL donnée par :

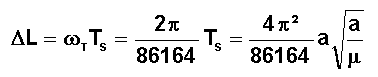
3°) Notion de phasage en képlérien:

En pratique certaines applications, notamment en surveillance militaire ou en imagerie spatiale, nécessitent que la trace se referme au bout d'un certain temps, de manière à survoler à nouveau le même lieu géographique de la terre.

Cette propriété s'appelle PHASAGE DE L'ORBITE. Le temps séparant 2 survols consécutifs d'un même lieu s'appelle PERIODE DE REPETITIVITE T_R.

En hypothèse képlérienne, T_R est un nombre entier n de période satellite T_S et nDL est congru à 0 modulo 2p. Si T_T désigne la période sidérale de la terre, le phasage se traduit par :

3°) Phasage non képlérien:

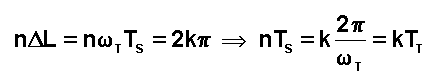
 En présence de perturbations, ce qui est le cas réel, les paramètres orbitaux ont des dérives séculaires. En particulier W et i varient, entraînant un mouvement Est-Ouest et Nord-Sud du plan orbital. La notion de phasage devient plus difficile. On convient de la définir à l'équateur au nœud ascendant.

• T_N désignera la période nodale, temps séparant 2 passages consécutifs au nœud ascendant. T_N est très légèrement différente de T_S à cause des perturbations.
• Par rapport au cas képlérien où le plan orbital est fixe, ici le plan orbital dérive autour de l'axe nord-sud, à une vitesse qui est la dérivée moyenne de W. Tout se passe comme si on changeait de vitesse angulaire w_T.

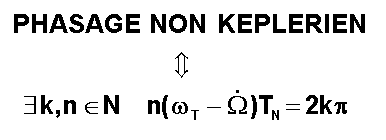
REMARQUE : Si on ne tient compte que de la perturbation due à la non sphéricité de la terre ( perturbation due à J2 ), et si on recherche l'héliosynchronisme, c'est à dire un choix de a et i de telle manière que la ligne des nœuds dérive exactement à la vitesse angulaire moyenne du soleil autour de la terre, alors la quantité ci-dessous vaut 1 jour de 24 h.

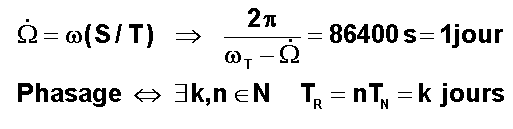
T_R est la période de répétitivité, un nombre entier de jours. C'est le cas de SPOT et de HELIOS.

IV VARIANTE POUR LE CALCUL DE LA TRACE

Nous exploitons ici les résultats de trigonométrie sphérique, qui vont permettre d'appréhender un peu mieux le calcul des points survolés par un satellite.

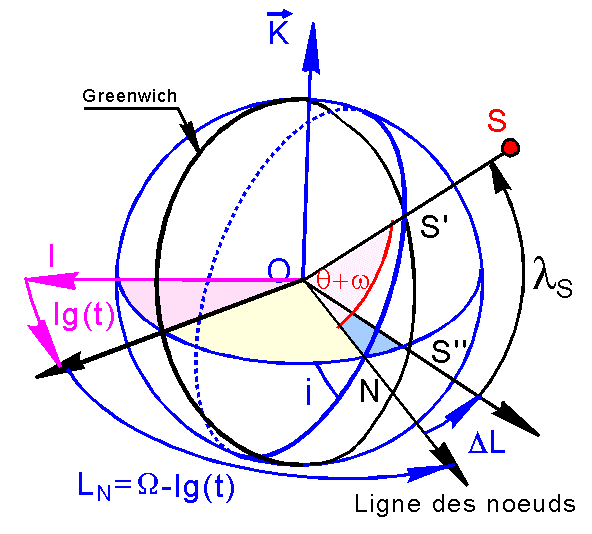
L'application des relations de trigonométrie sphérique dans le triangle rectangle S''NS' ( ~ABC ), donne :

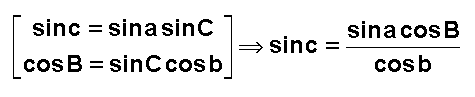
Moyennant les correspondances angulaires ci-dessous, on obtient :

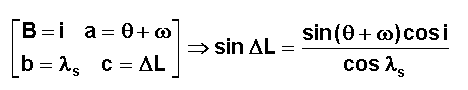
Il est clair que l'inversion qui conduit à DL ne pose pas de problème si q+w est entre -90° et +90°, mais peut poser problème dans le cas contraire. Il faut alors remarquer que le dessin doit être regardé depuis le nœud descendant. Le lecteur vérifiera alors l'affirmation suivante :

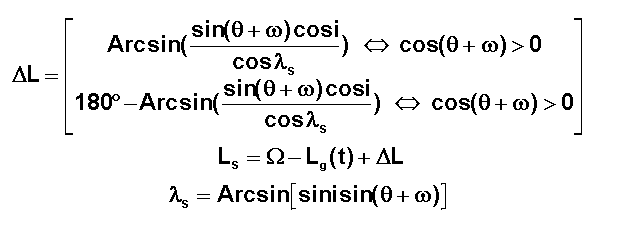
V LOGICIEL DE SIMULATION DE TRACES : :

Vous pouvez exécuter un programme nommé SOLSTICE, récupéré , avec autorisation explicite, pour simuler les trajectoires képlériennes de satellites existants ou ceux que vous pouvez créer, avec possibilité de liaisons vers des stations de votre choix.

Par correction, je n'ai pas rapatrié le téléchargement sur ce site, vous laissant le soin d'aller le chercher sur son site propriétaire ftp://trf.education.gouv.fr/pub/educnet/orbito/solstice9x.exe ( 8 Mo compressés et 26 MO après installation )

ESSAI ?

Guiziou Robert février 2002, sept 2011