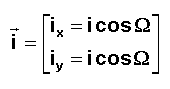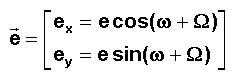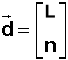|
CORRECTIONS ORBITALES DES PARAMETRES DE L'ORBITE GEOSTATIONNAIRE |
![]()
|
CONTENU : Mis à jour février 2003, sept 2011 I Problème des corrections orbitales |
|
![]()
Ce cours est le
prolongement naturel des équations de Gauss concernant les cas particuliers
d'orbite pour lesquelles: i voisin de 0 et e voisine de 0, avec comme
application naturelle, la maintenance des paramètres de l'orbite
géostationnaire et
les conséquences de corrections impulsionnelles de vitesse .
I PROBLEME
DES CORRECTIONS ORBITALES:
1°) Pourquoi des
corrections sont elles nécessaires ?
Le problème concerne tout
aussi bien :
Les manœuvres de mise à poste
fine d'un géostationnaire après le tir lanceur, l'injection et les orbites
intermédiaires de dérive.
En pratique les dispersions du moteur d'apogée, les erreurs
d'attitude du lanceur ... font que le satellite est sur une orbite légèrement
inclinée et excentrique, avec une longitude lo généralement à
quelques degrés à l'Ouest de la position visée. Le satellite conserve une
petite dérive do.
La correction périodique des
paramètres orbitaux dont l'évolution dépend des perturbations orbitales
Perturbation luni-solaire qui influe sur l'excentricité
Perturbation photonique agissant sur les panneaux solaires, pour
créer une force qui dans le temps agit sur l'excentricité.
Perturbations gravitationnelles dues à la Terre qui jouent en
particulier sur le moyen mouvement.
2°) Expression du
problème ?
Chaque satellite
géostationnaire suivant sa technologie et ses applications doit, pour assurer
sa mission, garder ses paramètres orbitaux dans une certaine plage de valeurs:
Notamment
la longitude de stationnement LS
L'inclinaison
pratiquement nulle, est réglée dans un intervalle non nécessairement centré en
0, de manière à positionner la valeur initiale en début ou fin de fenêtre,
suivant le sens des dérives séculaires connues.
L'excentricité
est de même calée dans un intervalle non nécessairement centré en 0, de manière
à ce que la valeur initiale soit en début ou fin de fenêtre, suivant le sens
des dérives séculaires.
3°) Equations
d'efficacité utilisées ?
Lorsque l'une
des conditions imposées aux paramètres n'est plus respectée, une séquence de MAINTIEN
A POSTE débute, consistant en un certain nombre d'impulsions de vitesse
algébrique DVi délivrées
en des points précis Mi de l'orbite d'ascension droite Si, à des instants ti,
permettant de ramener chaque paramètre à la valeur idéale de début de cycle de
fonctionnement.
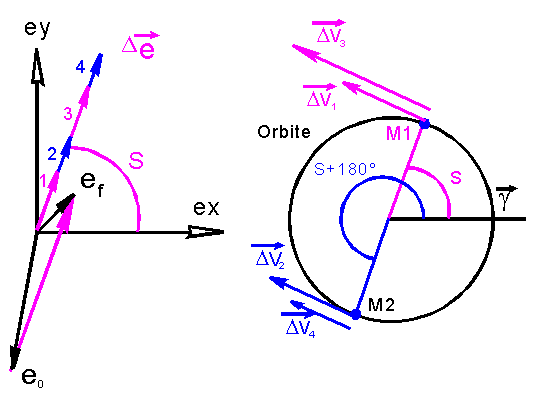
NB 1 : S = w + W + q ( q anomalie vraie )
NB 2 : Chaque allumage
d'une tuyère est suivi d'une restitution d'orbite afin d'affiner au mieux la
séquence suivante.
Le MAINTIEN
A POSTE commence à to et se termine à tf pouvant être plusieurs
jours après. La durée est un nombre entiers de jours.
Rappelons les équations de
contrôle établies dans un cours précédent, avec les notations classiques :
|
Vecteur inclinaison |
|
|
|
Vecteur excentricité |
|
|
|
Vecteur dérive |
|
L longitude moyenne n moyen mouvement |
|
Impulsion |
|
R vecteur radial, T orthoradial, N normal |

S est la longitude moyenne de la position où a lieu la
correction
Ce que les équations
nous montrent:
Propriété 1 ( P1 ): DVT permet de corriger l'EXCENTRICITE avec 2 fois plus
d'efficacité que DVR. On n'utilisera donc pas
d'impulsions radiales, ce faisant il faudra examiner ( voir plus loin ) de
plus près les moyens de la correction de la longitude moyenne l. On utilise alors le groupe d'équations :
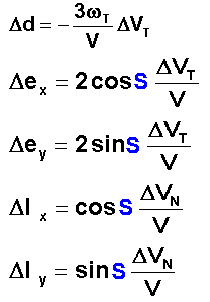
Propriété 2 ( P2 ): DVT permet de corriger simultanément la DERIVE et
l'EXCENTRICITE .
Propriété 3 ( P3 ): DVN corrige l'inclinaison i alors que DVT corrige l'EXCENTRICITE , il y a donc
quasi indépendance ( petit couplage dû à i ) entre les corrections Nord-Sud et
Est-Ouest, ce qui permet de programmer les premières quand on le souhaite. Pour
éviter le couplage résiduel éventuel, on corrige en plusieurs impulsions. Les corrections de l'inclinaison ne peuvent se faire
qu'en des points précis où S vaut ou S+p.
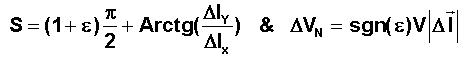
Propriété 4 ( P4 ): DVT qui corrige la dérive peut être programmée en tout point
de l'orbite, alors que les corrections de
l'excentricité ne peuvent se faire qu'en des points de l'orbite où l'incrément DVT est
normal au vecteur e, ce
qui fixe S. Ceci laisse le choix ( DVT,
S ) ou ( DVT , S+p ), augmentant le nombre de degrés de liberté des
manœuvres. Un dessin illustre le propos, avec la possibilité de délivrer
l'impulsion en M1 ou M2 .

NB : Il est clair que l'excentricité
peut être corrigée seule sans modifier d ou L par 2 impulsions opposées
en M1 et M2 de valeur absolue DVT/2.
Comment rétablir L sans
impulsion radiale ?
Il est clair que la dérive
d est la dérivée temporelle de la longitude moyenne . Or les corrections de
vitesse sont impulsionnelles, à des instants ti, donc la fonction
d(t) est une fonction en escalier, représentable par une somme de fonctions de
Heaveside. Sa primitive est donc une somme de fonctions linéaires du temps. La
dérive peut donc se corriger grâce à un "dosage" précis des
corrections tangentielles , de leur signe et du délai Dt = tf - to des opérations de
mise à poste.
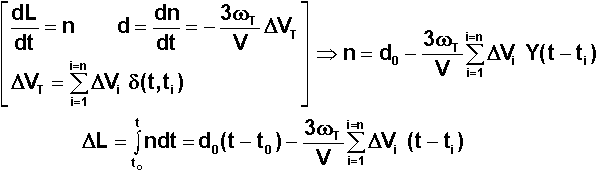
Donc sur la durée des
opérations on doit réaliser :
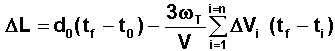
Nous verrons tout à
l'heure comment y parvenir.
II STRATEGIE
DE REPARTITION DES POUSSEES:
Nous supposons réalisées en
une ou plusieurs impulsions, la correction Nord-Sud du vecteur inclinaison.
Nous n'envisageons donc que des impulsions tangentielles positives ( sens de la
vitesse ) ou négatives ( sens contraire à la vitesse ).
1°) NOTION DE CORRECTION
OPTIMALE :
Nous dirons lorsque cette
condition est imposée, que le maintien d'orbite est optimisé ou optimal,
s'il minimise la fonction IMPULSION TOTALE :
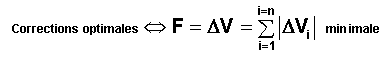
2°) NOTION DE COÛT
PREPONDERANT:
Oublions la correction
Nord-Sud pour n'envisager que celles Est-Ouest, qui doivent rétablir 4
quantités : d, ex, ey, L.
a) Coût en dérive :
Si l'on corrige la dérive d
seule, le coût maximum en impulsions de vitesse, quel que soit le nombre
d'impulsions est Cd. Les impulsions sont alors toutes de même signe et leur
position sur l'orbite peut être quelconque.

b) Coût en excentricité
:
Si l'on corrige l'excentricité
e seule, le coût maximum en impulsions de vitesse, quel que soit le nombre
d'impulsions est Ce. Les impulsions sont alors délivrées en des points précis
d'ascension droite S ou S+p, avec les signes convenables, comme vu plus haut.
c) Comparaison des coûts
:
Le coût total est donné
dans chaque cas par :
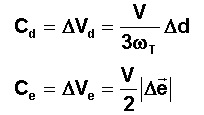
Naturellement ces coûts ne
sont pas égaux, sauf exception. Le plus grand est dit COÛT PREPONDERANT. En général c'est plutôt Ce
> Cd. C'est le coût prépondérant qui oriente la
stratégie.
a) Coût en excentricité
prépondérant Ce > Cd
3°) Corrections en 2
incréments de d et e ?
Quel
que soit le coût prépondérant nous avons 2 incréments de vitesse qui vérifient
: