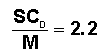FREINAGE ATMOSPHERIQUE

DUREE DE VIE

	Mise à jour 16 octobre 1999 I Freinage atmosphérique Forces de traînée et de portance Accélération perturbatrice Modèles et ordres de grandeur Evolution de l'orbite II Durée de vie d'un satellite Ordre de grandeur de la durée de vie Paramètres importants

Ce cours est consacré au calcul de l'effet de l'atmosphère sur l'orbite d'un satellite. Le freinage atmosphérique limite la durée de vie d'un satellite.

Là encore, il ne faut pas attendre une extrême précision dans la modélisation de l'atmosphère, tant celle-ci est sensible à l'activité solaire difficile à prévoir et fluctuante.

I FREINAGE ATMOSPHERIQUE :

La terre est entourée d'une couche de gaz en forme de bulbe, constituant l'atmosphère. Il est bien difficile de dire où l'atmosphère s'arrête.

1°) FORCES DE TRAÎNEE ET DE PORTANCE :

 La présence de molécules même très raréfiée dans un gaz peut produire un effet de traînée, si la vitesse du véhicule est très importante. Jusqu'à 1500 km l'effet peut être pris en compte.

Conventionnellement, on modélise l'effet de freinage d'un milieu gazeux, par une force dite de AERODYNAMIQUE qui se décompose en deux composantes:

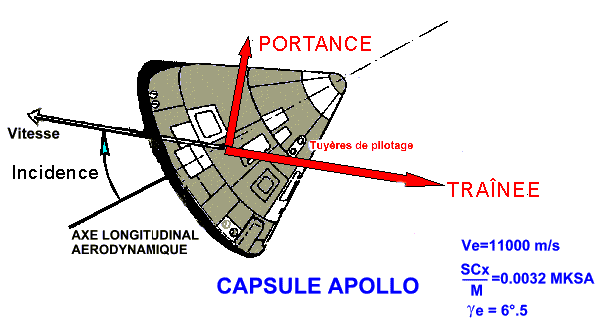
• L'une Rx, appelée TRAÎNEE, opposée au vecteur vitesse ( relative par rapport à l'atmosphère )
• L'autre Rz, appelée PORTANCE, normale au vecteur vitesse, dont le sens dépend de l'incidence i, sur la figure ci-dessous, l'incidence est dite >0 et la portance est vers le haut (vol sur le ventre). Si l'axe aérodynamique est "au dessus" du vecteur vitesse, la portance est vers le bas (vol dos).

On note conventionnellement ces deux forces :

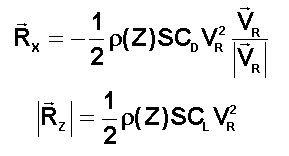
• Z désigne l'altitude terrestre sol (mais ce pourrait être une autre planète pourvue d'une atmosphère comme Mars ou Vénus )
• r(Z) est la fonction modélisation de l'atmosphère, dépendant de :
• Z dans les modèles simples, mais aussi pour des modèles plus élaborés de :
• L'activité solaire
• De l'heure, qui conditionne la position en rotation de la terre par rapport au soleil ( ombre ou soleil )
• De la latitude
• De la saison qui influence le flux solaire suivant l'hémisphère et la latitude.
• C_D et C_L des coefficients aérodynamiques dits de traînée ou de portance, dépendant du satellite et de sa forme notamment. Ces coefficients sont de l'ordre de 2 à 4.
• V_R est la vitesse relative du satellite par rapport à la masse d'air.

2°) ACCELERATION PERTURBATRICE :

Sauf pour des cas de rentrées atmosphériques où une portance est volontairement utilisée, en général on ne prend en compte que la seule traînée.

L'accélération perturbatrice s'obtient en divisant la force par la masse M, d'où :

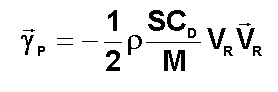
REMARQUE IMPORTANTE ET NON EVIDENTE A PRIORI :

Signalons ici, un résultat qui en général surprend le profane : celui qui est d'affirmer que plus un corps a des dimensions importantes, moins il est freiné. En effet l'accélération freinante a un module proportionnel à la quantité A = SC_D/M, qui est un coefficient de forme, appelé COEFFICIENT BALISTIQUE. Or la surface S du "maître couple" croît comme le carré de la dimension moyenne, alors que la masse croît comme le cube de la dimension moyenne. Il s'ensuit que A décroît quand la dimension moyenne croît. Ce phénomène est vérifiable pour toutes les pénétrations dans un fluide ou un gaz

• Sprinters de 100 ou 200 m, fortement charpentés
• Nageurs, skieurs de descente et descendeurs de km lancé sur neige
• Différence de distance d'arrêt d'un petit navire et d'un gros tanker, lorsque les moteurs sont coupés, etc...

Conclusion : les gros satellites sont moins perturbés que les microsatellites d'amateurs radio par exemple.

3°) MODELES ET ORDRES DE GRANDEUR :

a) Modèles de masse volumique de l'air :

Divers modèles sont utilisés, citons en deux parmi 8 ou 9 possibles ( voir ouvrages du CNES ):

• JACCHIA pour Z > 115 km
• CIRA88 pour Z <120 km, utiles pour les problèmes de retour d'engins ou de débris. Il apparaît comme le meilleur actuellement.
• Souvent en première approximation, on modélise l'évolution de la masse volumique de l'air, en utilisant des lois exponentielles, qui se raccordent par morceaux.

b) Quelques ordres de grandeur :

• Orbites basses : Z = 250 km avec r(Z) = 6.8 10^-11 kg/m³
• Orbites héliosynchrones de type SPOT : Z = 822 km avec r(Z) = 3 10 ^-14 kg/m³

c) Traînée :

• Pour SPOT à 822 km du sol, par exemple M = 1800 kg, S = 12 m², C_D = 2.7

On a V valant environ 7440 m/s et donc une perturbation d'accélération g_P = 1.5 10^-8 m/s².

• Ce même satellite à 250 km subirait g_P = 3.4 10^-5 m/s², ce qui est loin d'être négligeable.

4°) EFFETS SUR L'ORBITE :

De toute évidence, le freinage va dégrader l'énergie mécanique mE, qui diminue. Comme l'énergie spécifique décroît, le demi grand axe, en particulier diminue.

Les équations de Gauss montrent aussi, que l'excentricité décroît, il y a naturellement des effets sur d'autres paramètres orbitaux.

L'effet conjugué sur a et e, a pour effet le plus visible :

• Une circularisation de l'orbite
• Une diminution de l'altitude de l'apogée, plus importante que celle du périgée, car pour une orbite elliptique, le freinage est plus fort au périgée qu'à l'apogée ( Vitesse plus grande et masse volumique de l'air plus élevée aussi )
• Une diminution moindre du périgée.

L'ensemble des effets conduira le satellite non piloté, a rentrer dans les couches denses de l'atmosphère, pour y mourir brutalement calciné en quelques dizaines de minutes. Ceci nous amènera à parler de la durée de vie.

PARADOXE : Pour une orbite circulaire, il est facile de montrer à partir du théorème de l'énergie, que l'effet de la traînée, conduit non pas à une perte de vitesse, mais à une augmentation de celle-ci, parce que le rayon de l'orbite diminue constamment. D'où vient le surcroît d'énergie? Tout simplement de la récupération sur le potentiel gagné lors de la descente.

II DUREE DE VIE D'UN SATELLITE :

Il est clair que nous parlons ici de ce qu'il reste à "vivre" pour un satellite livré à lui-même, lorsque les opérations de maintenance d'orbite ne sont plus assurées. On appelle cette phase, la CHUTE du satellite.

Quelle que soit la finesse du modèle d'atmosphère, il est difficile de prévoir à un jour près, la durée de la chute. Il est tout aussi difficile de prévoir longtemps à l'avance, le point de chute sur le sol, d'éventuels débris. Ces prévisions ne peuvent se faire que dans les toutes dernières heures de la vie du satellite.

L'activité solaire dont le cycle est de 11 ans, et un flux pouvant varier de 80 à 200 KW/m² et le géomagnétisme de la terre, jouent beaucoup sur les prévisions.

Il faut de plus impérativement prendre en compte les perturbations d'orbite, qui font évoluer les paramètres orbitaux et donc notamment les périodes d'éclipse.

1°) Ordre de grandeur :

Donnons donc quelques valeurs approximatives :

	Altitude Z en km	Durée de vie en jours
	200	Quelques
	250	60
	300	220
	500	Quelques années
A titre indicatif	1000	Siècles
	1500	10000 ans

Le satellite Spot, vers 822 km, descend de 2.5 m/jour. Naturellement, il est surveillé et son altitude est régulièrement rétablie à sa valeur nominale.

2°) Paramètres importants :

L'expérience et les simulations montrent que les deux paramètres importants, sur la durée de vie, sont

• Le coefficient balistique
• L'activité solaire

Guiziou Robert 16 octobre 1999